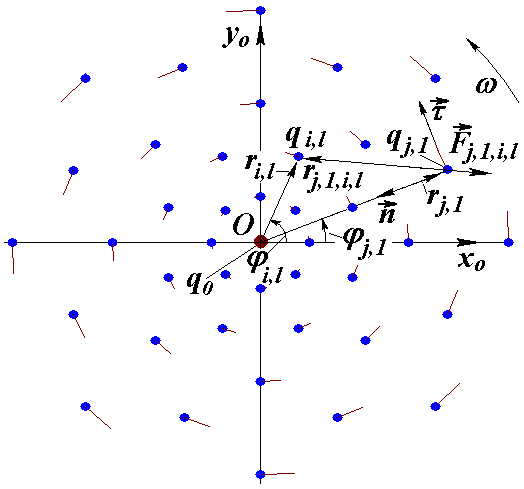
Рис. 1. Геометрические характеристики осесимметричной многослойной кулоновской структуры с параметрами: N2 = 5; N3 = 8; углы φj,1 первых тел на соседних кольцах чередуются.
Преамбула
Какой должна быть новая физика? Чем она должна отличаться от современной физики? В первую очередь она должна давать реальные представления о мире.
Объекты окружающего мира обладают разными свойствами, одним из главных является взаимодействие их друг с другом и движение. О явлениях макромира мы узнали многое благодаря тому, что поняли, какие объекты его порождают, как они взаимодействуют и как движутся. Например, о Солнечной Системе наши знания являются надежными в той части, в которой мы познали, из каких тел она состоит, как они взаимодействуют и движутся. В этой части мы можем сказать, что было с Солнечной системой миллионы лет назад и что с ней будет через миллионы лет в будущем. Благодаря таким знаниям человек обустраивает свою жизнь на Земле, начинает свою деятельность в космическом пространстве вокруг Земли. Со временем эта деятельность расширяется на другие тела Солнечной системы, а в будущем - и на тела вне Солнечной системы.
Точно также человек будет познавать микромир. Необходимо познать его реально существующие объекты. Рассмотреть взаимодействия между ними и изучить их движения.
Основными объектами микромира являются протон, электрон и нейтрон. Взаимодействия электрона и протона определяются законом Кулона. Как с помощью этих трех частиц образуется атом?
Разнородные атомы за счет кулоновского взаимодействия образуют молекулы всех веществ, которые есть в мире. При увеличении скорости движения частиц твердые вещества начинают плавиться и превращаться в жидкости. При дальнейшем увеличении скорости частиц жидкости превращаются в газы. Как это происходит?
Почему одни атомы, как водород, натрий, калий и др. очень активны и соединяются с другими атомами, и в природе по отдельности не существуют? А есть такие как гелий, аргон и др. Они, наоборот, с другими атомами не соединяются и в природе существуют только по отдельности. Почему одни атомы - стабильны и существуют вечно, а другие - неустойчивы и распадаются?
Чтобы ответить на эти вопросы, чтобы понять, как движения элементарных частиц протона, электрона и нейтрона приводит ко всем явлениям нашего мира, нужно изучать кулоновское взаимодействие между этими частицами.
В статье решен ряд математических проблем и создан набор методов для выполнения этой работы. В качестве примера рассмотрены плоские структуры из этих частиц, которые состоят из положительно заряженного ядра и отрицательных электронов, расположенных на нескольких концентрических слоях. Показано, как эти структуры создавать и как их изучать.
Все рассмотренные структуры долго не живут и разрушаются. В статье обсуждаются направления по поиску устойчивых структур.
Будут ли они найдены? Если да, то это будут атомы, и на все вышеупомянутые вопросы со временем мы получим ответы.
А если нет? Значит, микромир устроен по-другому. Но выполненные исследования не пропадут. Они подскажут, в каком направлении нужно идти дальше.
К какой области относятся эти исследования? Это механика, в частности механика микромира. В статье представлены начала механики микромира. Мы рассчитываем, что в процессе развития этой науки мы получим определенные и реальные знания о микромире.
Как читать эту работу? В ней рассмотрено много вопросов, использовано много разных методов и получено много новых представлений и результатов. Поэтому при первоначальном чтении нужно пробежаться по тексту и рисункам и понять, о чем идет речь. Спустя несколько дней, когда в голове все уляжется, более внимательно посмотреть работу. А дальше в зависимости от интересов, каждый для себя наметит программу изучения работы и использования ее результатов.
Кому будет полезна эта работа? Она может быть полезна студентам, интересующимся микромиром. Весь инструментарий имеется в свободном доступе http://www.ikz.ru/~smulski//Data/ClmRnStr/. Толковые студенты могут делать курсовые и дипломные работы. В последующем они могут перерасти в диссертации.
В физико-математических кружках способные ученики могут создавать свои модели атомов. Возможно, кто-то из них откроет действительную структуру атома. В этой работе им потребуется помощь их наставников: ряд используемых вопросов механики и математики в школе не изучают.
Для людей зрелых, интересующихся устройством мироздания, работа будет очень полезной. В ней они найдут подтверждения многим своим догадкам и предположениям, а где-то получат ответы, на возникавшие у них вопросы.
Не сомневаюсь, что работа будет полезна физикам, работающим с современными ускорителями, которые изучают взаимодействие ускоренных частиц с веществом. Они увидят, что интерпретация известных им явлений может быть совершенно другой, более логичной и естественной.
В завершения Преамбулы отвечу на вопрос, какой должна быть новая физика? Она должна быть основана на механике. На механике, которая идет от Ньютона. В 20-ом веке эта механика была испорчена. Ее основания я реанимировал в книге "Теория взаимодействия" http://www.ikz.ru/~smulski/TVfulA5_2.pdf. Тем, кому непонятно, что такое сила, масса, пространство и время, найдут в ней исчерпывающие объяснения.
Ссылка на статью: Смульский И.И. Плоские многослойные кулоновские структуры / Институт криосферы Земли СО РАН. - Тюмень, 2015. - 54 с. - Илл.: 35.- Библиогр.: 24 назв. - Рус. Деп . в ВИНИТИ 27.02.2015, № 38-В2015.
------------------------------------------------------------------------------------------------------------------
РОССИЙСКАЯ АКАДЕМИЯ НАУК
СИБИРСКОЕ ОТДЕЛЕНИЕ
ИНСТИТУТ КРИОСФЕРЫ ЗЕМЛИ
УДК 539.1.09 +521.1
И.И. Смульский
ПЛОСКИЕ МНОГОСЛОЙНЫЕ КУЛОНОВСКИЕ СТРУКТУРЫ
Тюмень 2015
-------------------------------------------------------------------------------------------------------------------
Деп. 27.02.2015, № 38-В2015.
Организация-депонент: Федеральное государственное бюджетное учреждение науки "Институт криосферы Земли" Сибирского отделения Российской академии наук, г. Тюмень
Название работы: Плоские многослойные кулоновские структуры
Автор: Смульский И.И., (13.04.1944), ФГБОУН "Институт криосферы Земли", г. Тюмень, Российская Федерация
Реферат: В работе сформулирована задача о вращающейся плоской многослойной структуре с кулоновским взаимодействием. Доказано отсутствие ее решений. На основе этой задачи разработан метод создания плоских структур с дифференциальным вращением слоев. Получен ряд структур, и численными методами, с помощью системы Galactica, исследована их динамика и устойчивость. Плоские структуры являются неустойчивыми. Намечены пути повышения устойчивости многослойных структур и создание таких, которые могли бы являться моделями атомов. Работа представляет интерес для специалистов в области механики микромира и может использоваться студентами при выполнении курсовых и дипломных работ.
Ключевые слова: кулоновские взаимодействия n-частиц, точные решения, многослойные структуры, численное интегрирование, динамика, устойчивость, модели атомов
Язык: рус.
Страниц: 54
Ил.: да
Библ.: 24
Title: Planar multilayer Coulomb's structures
Authors: Smulsky J.J., Institute of Earth's Cryosphere (IEC), Tyumen, Russian Federation
Abstract:
The author formulates the problem of a rotating planar multilayer structure with Coulomb interaction. The absence of its solutions is proven. Based on this problem the method of constructing planar structures with differential rotation of the layers is developed. A number of structures are received and their dynamics and stability are studied by numerical methods with assistance of the system Galactica. The planar structures are unstable. Identified ways to improve the stability of multilayer structures and constructing such, which could be models of atoms. The paper is of interest for specialists in the field of mechanics of microcosm and can be used by students when doing term papers and dissertations.
Key Words: Coulomb interaction of n-particles, the exact solution, multilayer structures, numerical integration, dynamics, stability, models of atoms
Аннотация
Для познания электронной оболочки атома необходимо выяснить движение электронов в ней. В работе рассмотрены движения в плоской модели атома. Решены задачи, которые позволяют задать координаты и скорости плоских многослойных кулоновских структур. Создана программа, с помощью которой получен ряд структур и подготовлены файлы начальных условий для системы Galactica. С ее помощью исследована динамика и устойчивость плоских многослойных структур. Они являются неустойчивыми. Намечены пути по созданию устойчивых моделей атома.
1. Введение
В современной физике кулоновское взаимодействие рассматривается на основе задачи двух тел. А поведение ансамблей частиц и их свойств в квантовой механике изучают в результате статистической обработки двухчастичных взаимодействий. Наряду с таким квантомеханическим рассмотрением микромира для объяснения ряда его явлений исследователи продолжают применять классическую механику. А.Д. Власов [1] в своих исследованиях пришел к выводу о справедливости законов классической электродинамики внутри атома и о несостоятельности вероятностной интерпретации внутриатомных явлений. Ф.М. Канарев [2]-[3] на основе классической физики объясняет спектры излучения атомов. М. Грызинский на протяжении нескольких десятилетий последовательно рассматривает явления микромира, основываясь на кулоновском механизме взаимодействия. Например, явления дифракции он объясняет прецессией спина электрона [4]. На основе бинарных кулоновских взаимодействий М. Грызинский рассматривает одинарную и двойную ионизацию, излучение одной или триплетной линий, дифракцию частиц при их рассеянии на атомах и молекулах [5]. Он показал, что учет воздействия электронной оболочки атома объясняет эффект К. Рамзауэра о слабом рассеянии электронов при малых их энергиях [6]-[7]. На основании классической механики М. Грызинский получил уравнения для определения абсолютной энергии торможения частиц произвольной средой во всем нерелятивистском спектре энергий [8].
Перечисленные результаты получены вышеупомянутыми исследователями аналитическими методами. Однако, все эти задачи сложны, и даже при высоком математическом уровне исследователя только отдельные задачи взаимодействия многих частиц могут быть решены. Поэтому использование высокоточных численных методов решения задач кулоновского взаимодействия открывает перспективу детерминированного познания микромира.
Для решения задач гравитационного а также кулоновского взаимодействий N частиц была создана система Galactica [9]-[11]. Она имеется в свободном доступе [12]-[13]. С помощью системы Galactica была рассмотрена [10]-[11] динамика и эволюция осесимметричной структуры [14], в центре которой находится положительно заряженная частица, вокруг которой по окружности равномерно расположены отрицательно заряженные частицы.
Известно, что в атомах электроны расположены на разных оболочках или слоях. Поэтому представляет интерес создание многослойных структур. Оказалось [15], что в случае гравитационного взаимодействия существует точное решение структуры из N2 слоев и N3 частиц в каждом слое, которая вращается как единое целое. Здесь N2 и N3 - любые целые числа. Представляет интерес решения аналогичной задачи для кулоновского взаимодействия.
Задачи, имеющие точное решение, позволяют определить положения и скорости частиц в начальный момент времени, т.е. рассчитать начальные условия (НУ). НУ необходимы для численного решения задачи N-частиц. В дальнейшем, в результате модификации таких НУ, можно получать НУ для любой конфигурации взаимодействующих частиц, а затем с помощью численного решения изучать их динамику и эволюцию.
2. Формулировка проблемы
Рис. 1. Геометрические характеристики осесимметричной многослойной кулоновской структуры с параметрами: N2 = 5; N3 = 8; углы φj,1 первых тел на соседних кольцах чередуются. |  |
В продолжение подхода, использованного в работах [14]-[15], в плоскости x0y0 рассматривается осесимметричная многослойная кулоновская структура (см. рис. 1). Она состоит из N2 слоев, на каждой из которых расположено N3 частиц. Совокупность частиц, центры которых расположены на одной окружности, будем называть слоем частиц. Номера слоев j = 1, 2 … N2 отсчитываются от центра, а номера частиц на каждом слое l = 1, 2 … N3 отсчитываются от оси x0 (рис. 1). В плоскости x0y0 обозначим rj,l и lj,l – полярные радиус и угол частица с электрическим зарядом qj,l. С целью упрощения в дальнейшем символом qj,l будем также обозначать и саму частицу. Все частицы одного слоя имеют одинаковый радиус rj,l = rj. Масса и заряд всех частиц, за исключением центральной, равны массе и заряду электрона: mj,l = me и qj,l = -e,соответственно, где e – модуль заряда электрона. Угол первой частицы на каждом кольце φj,1 определяет вид структуры. В дальнейшем он будет задаваться. А углы остальных периферийных частиц определяются по формуле
| φj,1 = φj,1 + (l - 1)·φ, | (1) |
где Δφ0 = 2π/N3 - угол между частицами на кольце.
Итак, геометрия осесимметричной многослойной структуры определяется количеством колец N2, количеством частиц на каждом кольце N3, радиусами колец rj и углами положения первых частиц φj,1. Суммарный электрический заряд частиц на всех слоях Z = -Zn·e, где зарядовый номер Zn всей структуры равен
| Zn = N2·N3. | (2) |
Заряд центральной частицы q0 = Zn·e, поэтому рассматриваемая структура является эдектрически нейтральной. Вся структура вращается с угловой скоростью ω. Тогда период вращающейся структуры Prd = 2π/ω. При задании параметров многослойной структуры: N2, N3, φj,1, Prd неизвестными являются радиусы слоев rj.
3. Силы взаимодействия частиц
Рассмотрим силы воздействия всех частиц на первую частицу qj,1 на слое j(см. рис. 1). С частицей qj,1 связываем траекторную систему координат (n,τ), где n - нормаль к траектории, а τ - касательная к ней. Сила Fj,1,i,l электростатического воздействия частицы qi,l, находящейся на кольце i, на частицу qj,1 определяется законом Кулона и в векторном виде запишется так:
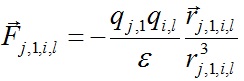 , , | (3) |
где εd - диэлектрическая проницаемость среды, в которой находятся частицы; rj,1,i,l = ri,l - rj,1 - расстояние частицы qi,l от частица qj,1. С учетом величин зарядов qj,1 и qi,l проекции силы Fj,1,i,l на оси 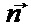 и
и 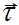 запишутся так:
запишутся так:
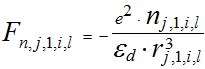 , , | (4) |
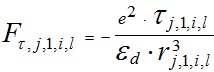 , , | (5) |
где nj,1,i,l и τj,1,i,l - проекции расстояния rj,1,i,l на оси координат n и τ , соответственно.
В треугольнике Oqi,lqj,1 (рис. 1) угол между радиусами частиц ri,l и rj,1 будет
| Δφj,1,i,l = φi,l - φ j,1, | (6) |
а расстояние между ними согласно теореме косинусов запишется так:
| rj,1,i,l2 = rj 2 + ri 2 - 2rirj cos Δφj,1,i,l. | (7) |
Тогда проекции этого расстояния на оси n и τ будут
| nj,1,i,l = -(ri cosΔφj,1,i,l - rj); τj,1,i,l = ri sinΔφj,1,i,l. | (8) |
Кроме периферийных частиц на частицу qj действует еще центральная частица с зарядом q0, которая находится в т. О (см. рис. 1). Проекция этой силы на ось равна нулю, а ее проекция на ось n запишется аналогично выражению (4):
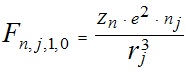 ,
,
где согласно (8) при ri =0 для центральной частицы nj = rj.
После подстановки (7) и (8) в выражения (4) и (5) и после суммирования сил по всем частицам структуры получаем выражения для проекций сил воздействия на частицу qj,1 всех остальных частиц:
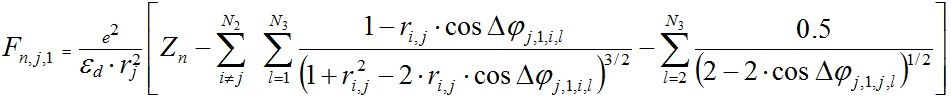 , , | (9) |
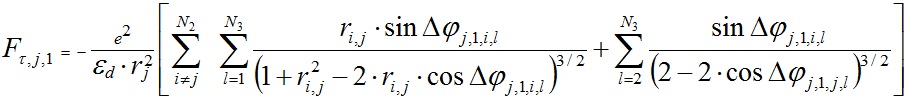 , , | (10) |
где ri,,j = ri/rj - отношение радиусов слоев i и j.
Чтобы исключить из рассмотрения силу воздействия частицы qj,1 на себя, в выражениях (9) и (10) воздействие остальных частиц j-того слоя извлечено из общего выражения и записано последним слагаемым. Оно легко получается при замене i на j в предыдущем слагаемом. В пределах суммирования исключение j-того слоя обозначено как i ≠ j.
Будем рассматривать такие конфигурации вращающихся структур, для которых выражения для силы (9) и (10) будут давать одну и ту же величину для каждой частицы j-го слоя. Это возможно только в том случае, если при прохождении оси n через любую частицу слоя j геометрические положения воздействующих частиц относительно нее не изменится. Последнее условие будет выполняться, если начальный угол частиц на кольцах будет принимать значение φj,1 = 0 либо φj,1 = 0.5·Δφ0. На рис. 1 представлен вид структуры, где значения начального угла φj,1 последовательно чередуются на соседних кольцах. Вышеуказанному условию удовлетворяют также структуры с произвольным порядком чередования начального угла φj,1.
Следует отметить, что вышеприведенные условия определяют использованный в работе термин "осесимметричный". Структура является осесимметричной, если ее геометрические и динамические характеристики не изменяются при повороте на угол равный Δφ0.
Для рассмотренных конфигураций нормаль n является осью симметрии (см. рис. 1). Поэтому углы отклонения Δφj,1,i,l воздействующих частиц от оси n имеют, согласно (6), попарно одинаковые по величине и обратные по знаку значения. Следовательно, в выражениях (10) синусы в числителях также попарно одинаковы по величине и обратные по знаку. Так как косинусы этих углов в знаменателях одинаковы, то касательные силы равны нулю. При четном количестве частиц N3 еще одно частица будет находиться на оси n симметрично относительно центра O. Так как угол Δφj,1,i,l этой частицы равен π, то сила ее воздействия в (10) также равна нулю. Итак, проекции всех сил на касательную ось равны нулю, т.е. Fτ,j,1 = 0. Поэтому сила воздействия всех частиц осесимметричной многослойной структуры на любую частицу на слое с номером j направлена по нормали n к траектории, т.е. к центру O, и определяется выражением (9).
Для кольца j разность углов, согласно (1) будет
| Δφj,1,j,l = φj,l - φj,1 = 2π(l - 1)/N3. | (11) |
Тогда выражение в знаменателе последнего слагаемого формулы (9) запишется
2 [1 - cos(2π(l - 1)/N3)] = 4 sin2(π(l - 1)/N3).
После подстановки этого выражения в (9) направленная к центру O (см. рис. 1) сила воздействия всех частиц на любую частицу на кольце j будет
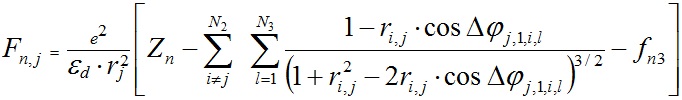 , , | (12) |
где
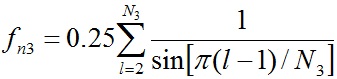 , , | (13) |
4. Уравнения движения вращающейся структуры
При воздействии с силой (12) на частицу qj,1 с массой me (рис. 1) она будет совершать ускоренное движение. В траекторной системе координат (n, τ) сила воздействия (12) имеется только вдоль одной оси n, по которой направлено нормальное ускорение wn = v2/ρ, где v - тангенциальная скорость движения частица qj,1, а ρ - радиус кривизны ее траектории. Поэтому дифференциальное уравнение ее движения запишется так
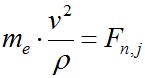 . . | (14) |
Мы рассматриваем вращающуюся структуру с угловой скоростью ω и с неизменными радиусами траектории. Поэтому для частицы qj,1 радиус кривизны траектории ρ = rj, а скорость v = ω·rj. После подстановки этих величин и силы (12) в дифференциальное уравнение движения (14) частицы qj,1 получаем следующее выражение для угловой скорости:
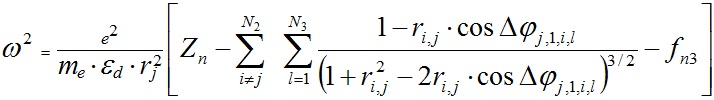 , , | (15) |
где j = 1, 2, N2.
Итак, движение частиц вращающейся структуры описывается N2 уравнениями (15). Это алгебраическая система уравнений. Как отмечалось ранее, неизвестными являются радиусы слоев rj. В отношении них система уравнений (15) является нелинейной. Перепишем ее в следующем виде:
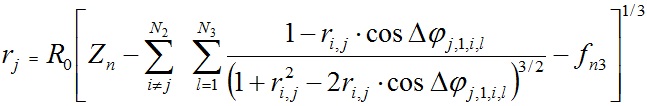 , j = 1, 2, N2, , j = 1, 2, N2, | (16) |
где
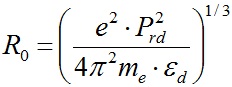 , , | (17) |
Prd - период вращающейся структуры.
5. Решение уравнений для однослойной структуры
Система N2 нелинейных уравнений (16) для радиусов слоев rj является неявной, так как в правые части входят радиусы rj. Если структура состоит из одного слоя N2 = 1, то согласно (2) Zn = N3, и из (16) получаем выражение для радиуса слоя
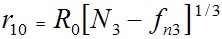 . . | (18) |
Итак, для однослойной структуры, вращающейся с периодом Prd, уравнения (16) дают решения (18) для радиуса слоя в явном виде. Радиус слоя r10 зависит от функции
| f2 = N3 - fn3. | (19) |
Согласно (12) для однослойной структуры (N2 = 1) сила воздействия всех частиц на периферийную частицу будет:
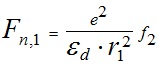 . . |
Таким образом, от функции f2 зависит сила воздействия на периферийную частицу и радиус слоя (18). На рис. 2 видно, что функция f2 имеет положительные значения до N3max = 472. А максимальное значение f2max = 27.651464 при N3opt = 174. Таким образом, однослойная осесимметричная структура из положительно заряженного ядра и равномерно расположенных по окружности электронов может существовать при их числе N3 ≤ 472. При большем числе электронов силы отталкивания между электронами превышают силу их притяжения к ядру. Наиболее оптимальное соотношение между силами притяжения и отталкивания при количестве электронов N3 = 174. В этом случае, например, сила воздействия ядра на периферийную частицу в 15.8 раз больше, чем в случае слоя из двух частиц при одинаковых радиусах слоев.
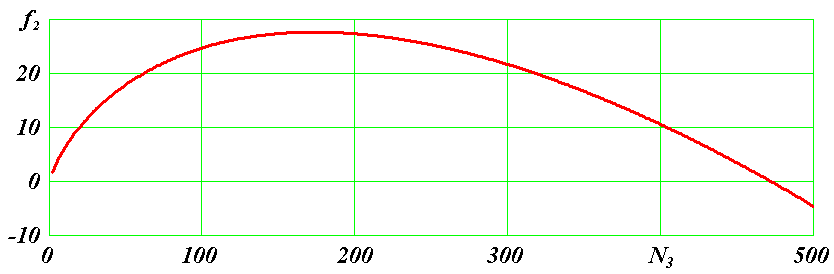
Рис. 2. Зависимость функции f2 от количества частиц N3 в слое.
Рассмотренные свойства однослойной структуры справедливы в статике. В процессе ее вращательного движения небольшие возмущения приводят к смещению частиц от их осесимметричного расположения [10]-[11], которые нарастают, и структура разрушается после нескольких оборотов. Поэтому такие плоские структуры даже с двумя периферийными электронами являются неустойчивыми [10]-[11].
Представленные на рис. 2 свойства функции f2 показывают, что в кулоновских нейтральных структурах с центральным положительным ядром при определенном количестве электронов сила отталкивания между ними начинает превышать силу притяжения к ядру. По-видимому, это является причиной того, что существует предел в количестве электронов в таких структурах, как атомы. Например, в одном из последних элементов, менделевии, с зарядовым числом Z = 101 количество электронов равно 101. В плоской осесимметричной структуре с одним слоем, как отмечено выше, предельное число электронов - 474, т.е. в 4.7 раза больше. Однако, такие структуры неустойчивы и существовать не могут. По-видимому, устойчивая конфигурация должна быть многослойной.
6. Метод решения уравнений для многослойных вращающихся структур
Перепишем систему уравнений (16) в следующем виде:
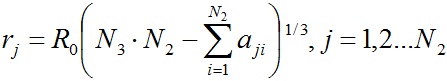 , , | (20) |
где
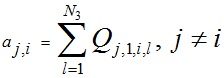 ; ; | (21) |
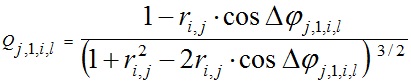 ; ; | (22) |
| aj,j = fn3. | (23) |
Как уже отмечалось, точные значения радиусов слоев структуры определяются нелинейной системой уравнений (20), в которых коэффициенты aj,i описаны выражением (21) при j ≠ i, а для случая j = i - выражением (23). Далее рассмотрим способ решения этой системы.
В случае двухслойной структуры из уравнения (20) для радиуса второго слоя r2 следует, что он будет зависеть от радиуса r1 первого слоя. Поэтому, если радиус r1 определить по радиусу r10 однослойной структуры, то можно приближенно рассчитать и радиус r2 второго слоя. Из анализа сил взаимодействия между частицами установлено [15]-[17], что воздействие частиц внешних слоев на частицы внутренних слоев почти взаимно уравновешивается. Поэтому определение радиусов r1 и r2 рассмотренным выше образом даст результаты с небольшими отличиями от точных решений уравнений (20). Эти рассуждения применимы для трехслойной, четырехслойной и т.д. структур. Таким образом, в первом приближении можно определить радиусы rj1 структуры с любым количеством слоев. Затем rj1 могут быть уточнены в результате итерационного процесса.
Запишем алгоритм рассмотренного способа решения. В первом приближении радиусы слоев последовательно определяются по формулам для структур с увеличивающимся количеством слоев
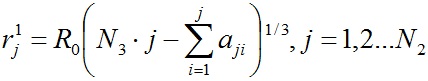 . . | (24) |
Затем с помощью уравнений (20) определяются последующие приближения: rj2, rj3, … rjk. После каждой итерации рассчитываются невязки по уравнениям
| Vjk = (rjk - rjk-1)/R0 | (25) |
и суммарная невязка
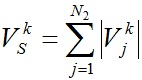 . . | (26) |
После достижения условия
| VSK ≤ EPS, | (27) |
где EPS - заданная погрешность, итерационный процесс заканчивается.
Этот алгоритм реализован в программе RtStClb.for на языке FORTRAN. В файле RtStClb.dat задаются входные параметры структуры, в том числе N2, N3, φj,1, Prd, EPS. Следует отметить, что в программе не используются индексы в наименовании переменных, т.е. вместо Prd используется Prd. После работы исполняемого модуля программы RtStClb.exe создается несколько файлов с результатами, в том числе файл со всеми кинетическими параметрами структуры. Этот файл содержит исходные данные и начальные условия для модуля кулоновского взаимодействия системы Galactica [12]-[13]. Система Galactica позволяет рассчитать динамику структуры и исследовать ее эволюцию.
7. Исследования по созданию многослойных вращающихся кулоновских структур
С помощью программы RtStClb.exe были выполнены исследования по созданию вращающихся структур при вариации параметров N2, N3, φj,1 и Prd при погрешности EPS = 10-12. С целью проверки алгоритма была рассчитана однослойная структура с параметрами атома кислорода [10]-[11] при N2 = 1 и N3 = 8. Кинематические параметры ее совпали с аналогичной структурой, но рассчитанной другим способом [10]-[11].
В процессе исследований были получены решения уравнений (20) для двухслойных структур N2 = 2 с числом тел N3 = 2, 3, 4, 5, 6. При этом для структуры с N3 = 2 решения получены с тремя разными периодами Prd вращения: 0.1; 0.5; 5 в единицах времени UnT = 10-15 сек. Углы первых частиц на слоях чередовались φj,1 = 0 и φj,1 = Δ φ0. Решений для структур с большим числом слоев не было получено.
Во всех решениях для двухслойных структур радиусы первого и второго слоя оказались равными. Таким образом, по существу эти решения дали однослойные структуры с количеством частиц в слое 2·N3.
Для гравитационного взаимодействия многослойные вращающиеся структуры существуют при любых значениях N2 и N3 [16]. А для кулоновского - вращающаяся структура может быть только однослойной. Этот вывод следует из вышеприведенных численных исследований. Однако численные исследования не могут охватывать все возможные ситуации. Поэтому рассмотрим эту задачу приближенно, но аналитически. Как уже упоминалось, воздействие частиц, расположенных на внешних слоях, на частицу на внутреннем слое почти уравновешивается [15]-[17]. Поэтому пренебрегаем их воздействием, а воздействие частиц на внутренних слоях рассматриваем также приближенно. Будем считать, что на частицу q1,j, находящуюся на j-том слое, воздействует частицы j-того слоя и новое ядро, заряд которого уменьшен на суммарный заряд электронов внутренних слоев
| Zj = [Zn - (j-1) N3]e. | (28) |
Тогда после замены в (15) Zn·e на Zj и в пренебрежении слагаемым воздействия других слоев угловую скорость вращения j-того слоя получаем в следующем виде:
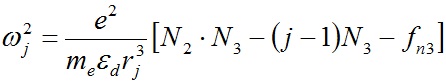 , , | (29) |
где использовано выражение для зарядового номера структуры Zn = N2 N3.
Угловая скорость вращения первого слоя j = 1, согласно (29), запишется
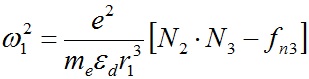 . . | (30) |
Разделив (29) на (30), угловую скорость для j-того слоя (29) запишем в относительных единицах:
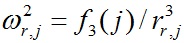 , , | (31) |
где 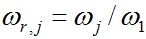 ;
; 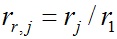 - угловая скорость и радиус j-того слоя, отнесенные к соответствующим величинам первого слоя;
- угловая скорость и радиус j-того слоя, отнесенные к соответствующим величинам первого слоя;
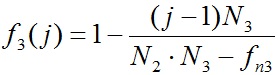 . . | (32) |
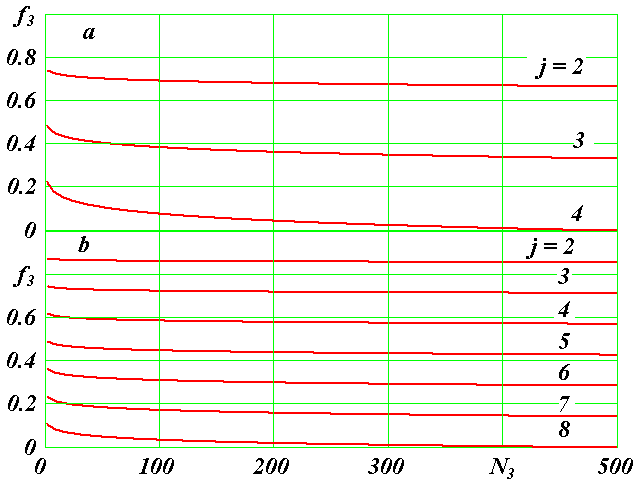
Рис. 3. Изменение функции f3(j) для разных слоев j в зависимости от количества частиц N3 в слое для четырехслойной структуры (a) и восьмислойной (b).
Чем больше номер j слоя, тем больше его радиус rj. Тогда при постоянной функции f3(j) = 1 из выражения (31) следует, что угловые скорости слоев с удалением их от центра будут уменьшаться. Например, при rr,j = 1, 2, 3 квадраты угловых скоростей будут 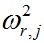 = 1, 1/8, 1/27. На рис. 3 представлено изменение функции f3(j) при разных N2 и N3. Во-первых, функция f3(j) < 1, а во-вторых, она уменьшается с увеличением номера слоя j. Таким образом, функция f3(j) будет приводить к еще более сильному падению угловых скоростей наружных слоев.
= 1, 1/8, 1/27. На рис. 3 представлено изменение функции f3(j) при разных N2 и N3. Во-первых, функция f3(j) < 1, а во-вторых, она уменьшается с увеличением номера слоя j. Таким образом, функция f3(j) будет приводить к еще более сильному падению угловых скоростей наружных слоев.
Итак, в многослойной структуре угловая скорость слоев уменьшается с удалением слоя от центра. Поэтому она не может быть одинаковой для всех слоев, в связи с чем, невозможно создать структуру с одинаковой скоростью вращения слоев.
8. Многослойные структуры с дифференциальным вращением слоев
В связи с невозможностью создания многослойной кулоновской структуры, вращающейся как единое целое, рассмотрим структуры с разными угловыми скоростями слоев. Пусть они в начальный момент времени имеют осесимметричную конфигурацию. Поэтому для них справедлива геометрия, представленная на рис. 1, и полученные уравнения (15) и (20) для угловой скорости и радиуса слоя. Однако вращение слоев происходит с разными угловыми скоростями ωj, поэтому в дальнейшем осесимметричная форма структуры нарушается. Таким образом, полученные выражения позволяют определить координаты и скорости многослойной структуры в начальный момент времени. Эти параметры будут являться начальными условиями для исследования динамики и эволюции многослойной структуры в результате интегрирования дифференциальных уравнений движения составляющих ее частиц. Как уже упоминалось, для этих целей создан модуль кулоновского взаимодействия системы Galactica [13].
Запишем основные выражения для расчета многослойных структур с дифференциальным вращением слоев. В этом случае периоды Prdj и угловные скорости ωj слоев будут разными. Параметр R0, согласно выражению (17), также зависит от Prdj. С учетом этого, выразим из (20) период вращения
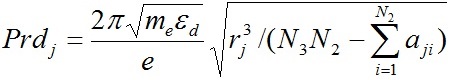 . . | (33) |
Выражение (33) позволяет определить периоды обращения слоев многослойной структуры, если известны их радиусы. Для решения конкретных задач нахождение радиусов rj представляет определенную сложность. С целью ее преодоления задается начальный период вращения первого кольца Prdi и по нему согласно (17) определяется параметр R0
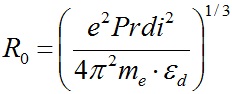 . . | (34) |
Если выразить Prdi из (34) и выражение (33) отнести к Prdi, то получим уравнение для периодов слоев в безразмерных величинах
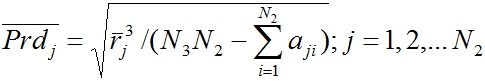 , , | (35) |
где 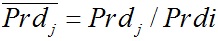 ;
; 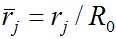 - безразмерные период вращения слоя j и его радиус, соответственно.
- безразмерные период вращения слоя j и его радиус, соответственно.
Выражениями (35) определяются периоды вращения слоев, безразмерные радиусы 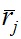 которых могут быть заданы в единицах R0. В рассмотренном далее алгоритме радиус первого кольца рассчитывается по (20) в пренебрежении воздействием наружных колец:
которых могут быть заданы в единицах R0. В рассмотренном далее алгоритме радиус первого кольца рассчитывается по (20) в пренебрежении воздействием наружных колец:
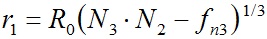 . . | (36) |
А радиусы остальных колец rj могут быть заданы по любому алгоритму на основании r1.
Координаты частиц структуры в начальный момент времени определяются радиусами rj и углами положения частиц φj,l, а их скорости - периодами Prdj вращения слоев [10]-[11]. Из выражения (35) для периодов видно, что при определенных коэффициентах aji знаменатель может быть отрицательным, поэтому величина периода Prdj будет мнимой, т.е. структура с такими параметрами не может быть создана. Как отмечалось ранее, эта ситуация обусловлена тем, что на каком-то слое сила отталкивания электронов превышает силу их притяжения к ядру. Из выражений (21) - (22) для параметра aji видно, что он зависит от соотношения радиусов rij = ri/rj, разности углов Δφj,1,i,l, числа колец N2 и числа частиц N3 на них. Поэтому поиск структур, которые в знаменателе (35) не давали бы отрицательных значений, представляет не простую проблему.
Для выполнения расчетов и создания файлов начальных условий разработана программа RtStClb2.for на языке FORTRAN. В файле RtStClb2.dat задаются параметры структуры, в том числе: N2, N3, φj,1, Prdi и необходимые константы, например, массы электрона, протона и нейтрона. После работы исполняемого модуля RtStClb2.exe создается несколько файлов с результатами, в том числе файл с начальными условиями для системы Galactica. В Приложении представлено описание программы RtStClb2.for и ее работы, содержание файла исходных данных RtStClb2.dat и текст программы.
С помощью программы RtStClb2.exe были выполнены исследования по созданию структур, в которых ядро состояло из одинакового количества нейтронов и протонов. По мере освоения программы было проведено несколько серий исследований. Первоначально безразмерные радиусы задавались по линейному закону:
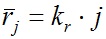 . . | (37) |
где kr = 1. А исходный период был Prdi = 3.29471·10-17 сек.
В этих структурах период вращения слоев определялся без учета воздействия наружных слоев, т.е. он рассчитывался по формуле:
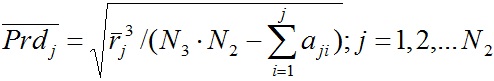 . . | (38) |
в которой суммирование идет от 1 до номера слоя j, а не до номера последнего слоям N2, как в формуле (33).
Были получены структуры с тремя конфигурациями: одна структура с N2 = 2 и N3 = 8 при φj,1 = 0; две структуры с чередованием φj,1: трехслойная с N3 = 8 и четырехслойная с N3 = 6. Кроме того, последняя структура (N2 = 4 и N3 = 6) была создана при других радиусах слоев: kr = 1.5 и 2, а также при других исходных периодах Prdi = 1·10-15 сек и 1·10-17 сек. Таким образом, у рассмотренных трех конфигураций структур радиусы и периоды могут изменяться в широких пределах.
В последующих сериях периоды вращения слоев рассчитывались по формуле (33). Кроме вышеупомянутых структур были получены двухслойные структуры с числом частиц до N3 = 100 при φj,l = 0 и с чередованием φj,l = 0 и φj,1 = Δφ0. В последующем эти структуры были получены и для первого случая.
В третьей серии исследований радиус структур задавался в дополнительном файле RtNcJR01.dat, который подключался к файлу исходных данных RtStClb2.dat. В этом случае структуры были получены следующим образом. Если при каких-либо параметрах структура не создавалась, то после исполнения программы RtStClb2.exe появлялось сообщение об отрицательном знаменателе в выражении (33) для какого-либо слоя j. Для этого слоя радиус rj изменялся, как правило, увеличивался. Затем номера слоев j и радиусы rj задавались в файле RtNcJR01.dat. Таким образом, были получены двухслойные структуры с числом частиц N2 > 100, например, N2 = 150, и четырехслойная структура с N2 = 4 и N3 = 8.
При исследовании вращающихся структур с гравитационным взаимодействием [16] были получены структуры, в которых соседние слои имели одинаковые радиусы. В случае кулоновского взаимодействия рассмотренным выше образом была создана такая структура с N2 = 5 и N3 = 8. В ней попарно одинаковые радиусы были у 2-го и 3-го , 4-го и 5-го колец. Углы φj,1 у колец с одинаковыми радиусами были разные. Поэтому эти сдвоенные кольца образовывали слои с удвоенным числом частиц. Таким образом, рассматриваемая структура имела три слоя, из которых первый имел 8 частиц, а остальные по 16. Следует отметить, что изображения ряда из этих структур будут ниже представлены.
9. Динамика четырехслойной структуры
Была исследована динамика четырехслойной структуры с N3 = 6; kr = 1, Prdi = 3.29471·10-17 сек (см. рис. 4). На каждом слое осесимметрично расположено 6 электронов. Общий заряд всех электронов qSe = -24·e, где e - модуль заряда электрона. Центральная частица 0 состоит из 24 нейтронов и 24 протонов, т.е. вся структура электрически нейтральна. Относительные радиусы слоев и периоды 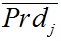 приведены в табл. 1. Как уже отмечалось, здесь исследуется структура, периоды вращения слоев в которой рассчитывались по формуле (38). Для сравнения в табл. 1 даны периоды
приведены в табл. 1. Как уже отмечалось, здесь исследуется структура, периоды вращения слоев в которой рассчитывались по формуле (38). Для сравнения в табл. 1 даны периоды 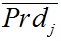 , рассчитанные по формуле (33). Как видно, учет воздействия наружных слоев приводит к уменьшению периода вращения у внутренних слоев, и тем больше, чем ближе слой находится к центру.
, рассчитанные по формуле (33). Как видно, учет воздействия наружных слоев приводит к уменьшению периода вращения у внутренних слоев, и тем больше, чем ближе слой находится к центру.
Таблица 1. Рассчитанные радиусы слоев 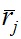 и периоды их обращения
и периоды их обращения 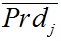 четырехслойной структуры при R0 = 1.90959·10-11 м и Prdi = 3.29471·10-17 сек, а также относительные радиусы слоев rj/Am при исследовании динамики структуры программой Galactica.
четырехслойной структуры при R0 = 1.90959·10-11 м и Prdi = 3.29471·10-17 сек, а также относительные радиусы слоев rj/Am при исследовании динамики структуры программой Galactica.
| № слоя, j | 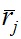 | 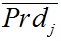 , (38) , (38) | 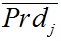 , (33) , (33) | rj/Am, Galactica | |
| T = 0 | T = 0.2245 | ||||
| 1 | 2.809 | 1 | 0.988 | 3.77 | 3.8 |
| 2 | 5.619 | 3.434 | 3.310 | 7.55 | 8.16 |
| 3 | 8.428 | 8.513 | 8.433 | 11.32 | 11.60 |
| 4 | 11.237 | 35.037 | 35.037 | 15.1 | 30.17 |
Динамика структуры исследовалась в результате решения дифференциальных уравнений движения ее частиц с помощью системы Galactica. На рис. 4 показана несколько модифицированная выдача программы Galactica на экране монитора результатов этой задачи после первого шага с ΔT = 1·10-10. Линиями у периферийных частиц представлены их вектора скорости, а числами даны: время T = 1·10-10; наибольшая масса m0max = 0.99972…; модуль наибольшей скорости vmax = 719.8…; исполненный шаг счета ΔTp = 1·10-10; проекции количества движения структуры: Px, Py, Pz; проекции момента количества движения структуры: Mx, My, Mz. Описание остальных параметров представлено в [9] и [13]. Последними двумя числами даны величина заданного шага счета ΔT = 1·10-7 и относительное изменение z-составляющей суммарного момента количества движения δMz = 0, где δMz = (Mz-Mz1)/Mz1; Mz1 - момент количества движения на первом шаге счета. Задача решается в безразмерных параметрах: масса частиц отнесена к массе всей структуры mSS, время к единице времени UnT = 1·10-15 сек, длина к Am = 1.421·10-11 м, а заряд частиц - к e.
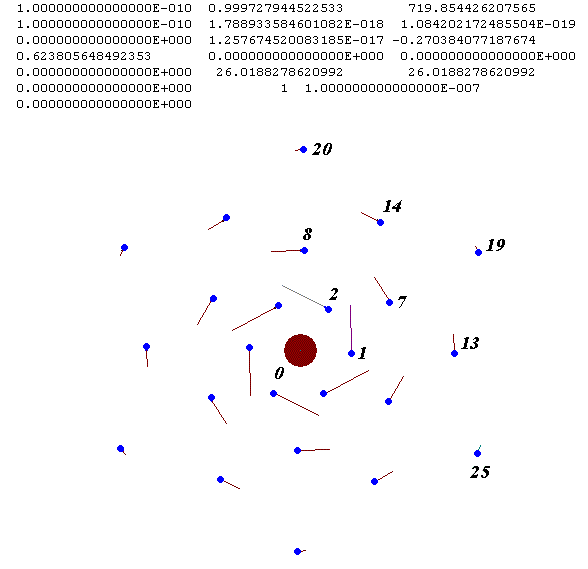
Рис. 4. Вид четырехслойной структуры на экране дисплея при решении задачи о ее движении с помощью системы Galactica: 0 - центральная частица; 1- 2 -частицы первого слоя; 7 - 8 -частицы второго слоя; 13 - 14 - частицы третьего слоя; 19, 20 и 25 -частицы четвертого слоя. Числами дана характеристика динамики и вычислительного процесса структуры [13] в момент T = 1·10-10.
В процессе решения задачи по экрану дисплея можно наблюдать за развитием структуры. Как и следует из табл. 1, слои вращаются с разными скоростями: внутренний слой быстрее, а наружные - медленнее. До 7 оборотов внутреннего слоя (T ≈ 0.215) видимых изменений структуры, за исключением увеличения размера наружного слоя, не наблюдается. На восьмом обороте начинаются заметные изменения в структуре (рис. 5). Внутреннее кольцо распадается на три пары частиц, которые имеют разные расстояния от центральной частицы. Кроме того, радиус орбиты четвертого, наружного, слоя, увеличился вдвое (табл. 1), а радиусы остальных слоев практически не изменились. При T = 0.306 одна из частиц приближается к центру, достигает скорости 4.268·106 и выбрасывается из структуры. Этот момент можно считать концом ее жизни.

Рис. 5. Начало разрушения четырехслойной структуры при T = 0.2245. Обозначение см. на рис. 4.
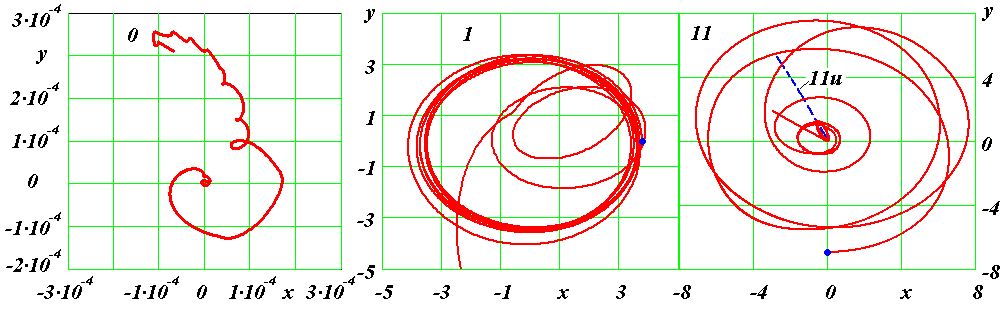
Рис. 6. Траектории в экваториальной плоскости до момента T = 0.306; 0 - центральная частица; 1 - первая частица первого слоя; 11 - предпоследняя частица 2-ого слоя; точками отмечены положения частиц при T = 0; 11u - уточненный расчет с момента T = 0.3048999 до T = 0.3096261.
На рис. 6 показаны проекции траекторий на плоскость xy, которая повернута относительно оси x0 на угол ε = 0.4010. С целью контроля точности вычислений плоское движение частиц многослойной структуры в программе Galactica рассматривается в трехмерной системе координат xyz. Величина угла ε взята равной наклону плоскости экватора Земли к плоскости ее орбиты. Поэтому она названа экваториальной. На рис. 6 показаны траектории центральной частицы 0, частицы 1 первого слоя и частицы 11 второго слоя. Движение центральной частицы 0 за время T = 0.306 происходит в области размером порядка 3·10-4, т.е. достаточно малой по сравнению с диаметром структуры, равного порядка 90 безразмерных единиц. Частица 1 первого слоя из начального состояния, отмеченного точкой на рис. 6, совершает 7 обращений по траектории, которая слегка изменяется. Затем размер ее орбиты уменьшается в два раза. Совершив по ней одно обращение, она снова переходит на орбиту с меньшим радиусом. После двух обращений по ней виден излом в траектории, после которого частица переходит на эллиптическую траекторию с большим эксцентриситетом. Излом в траектории частицы 1 обусловлен ее взаимодействием с другой частицей при их сближении.
Частица 11 из начального состояния, отмеченного точкой на рис. 6, совершает два обращения по непрерывно изменяющейся орбите. Затем ее орбита уменьшается в два раза. После одного обращения по ней она переходит снова на уменьшенную в два раза орбиту. После двух обращений по ней орбита частицы 11 уменьшается еще в несколько раз, и после 5 обращений по ней, как видно из рис. 7, она приближается к центральной частице, достигает скорости 4.268·106, а затем выбрасывается из структуры.
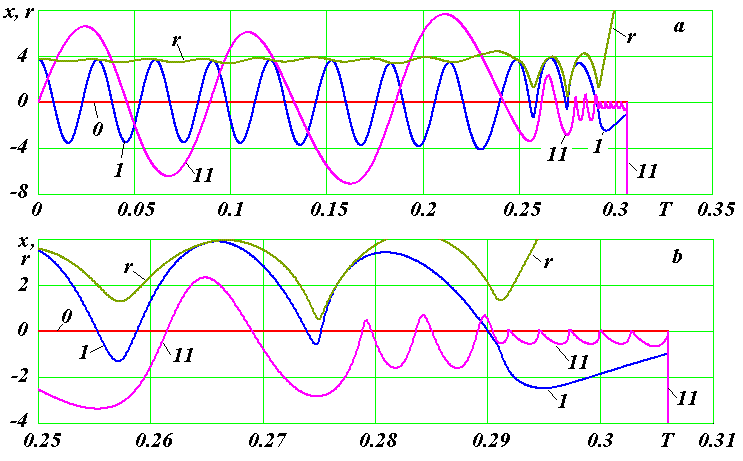
Рис. 7. Изменение координаты x во времени центральной частицы 0 и двух периферийных частиц 1 и 11, а также радиуса орбиты r частицы 1: a - на интервале T = 0 ÷ 0.306; b - в увеличенном масштабе.
На рис. 7 эти движения показаны на законах движения x(T) этих частиц за время T = 0.306. Здесь также линией r показано изменение расстояния частицы 1 от начала координат. Волнистый характер изменения r на первых семи ее обращениях свидетельствует, что орбита этой частицы является эллипсом с небольшим эксцентриситетом. Это небольшое отличие окружности от эллипса свидетельствует, с какой точностью рассмотренный ранее алгоритм (33)-(35) определения периода вращения слоя, а по нему задания начальных скоростей частиц реализуется для первого слоя. По малому изменению радиусов орбит второго и третьего слоя (табл. 1) за время T = 0.2245 видно, начальные скорости этих слоев также заданы хорошо. В тоже время увеличение в два раза радиуса четвертого слоя свидетельствует, что алгоритм (33)-(35) дает для него завышенные скорости.
Изменение координаты x частицы 1 на рис. 7b демонстрируют отмеченные ранее изменения. А по изменениям координат x частицы 11 в увеличенном масштабе видны все последовательные изменения ее орбиты, а также траектория ее выброса из структуры.
Выброс частицы из структуры происходит при достижении частицей большой скорости. В случае гравитационного взаимодействия многих частиц также наблюдается выброс одной [15] или нескольких частиц. Большую скорость частица приобретает при сближении с другой частицей на малое расстояние. При кулоновском взаимодействии сближение электронов не приводит к увеличению скорости, так как они взаимно отталкиваются. Поэтому периферийная частица в рассматриваемых структурах может приобрести большую скорость при ее близком прохождении у центральной частицы. Чтобы выяснить механизм выброса частицы из структуры, были выполнены детальные исследования. В системе Galactica имеются разные режимы, которые позволяют визуально на экране дисплея в разных масштабах и ракурсах наблюдать за взаимодействием частиц, получить параметры сближений заданной частицы с другими частицами, исследовать траектории частиц относительно начала координат или относительно одной из них и т.д. Эти средства были использованы для исследования механизма выброса частицы из структуры.
В момент T = 0.25 частица 11 после сближения с частицей 16 на расстояние r = 2.89 (см. рис. 7) перешла на орбиту с меньшим радиусом. Процесс уменьшения ее орбиты происходил под воздействием частицы 2. Дальнейшее уменьшение орбиты в момент T = 0.275 произошло от сближения с частицей 12 на расстоянии r = 1.43. В момент T = 0.29084 частица 11 сближается с частицей 1 на расстояние r = 0.151. После этого она переходит на орбиту с наименьшим радиусом (см. рис. 7b), а частица 1, как видно из рис. 6, испытывает излом в траектории и уходит на траекторию с большим эксцентриситетом.
После пяти обращений частицы 11 (рис. 7b) по своей наименьшей орбите она сближается с частицей 5 в момент T = 0.304264 на расстояние 0.2804, после чего частица 11 уходит со своей траектории и устремляется к центру.
Отмеченные характеристики движения частицы 11 установлены по данным сближения частицы, которые могут быть получены в системе Galactica. На рис. 8 эти данные представлены графически в виде минимального расстояния Rmin между частицей 11 и другими частицами. Каждая точка линии Rmin представляет собой минимальное расстояние за время интервала ΔTin = Kl3·ΔTi = 3·10-4, а величинами Np отмечены номера частиц, с которыми произошло сближение. Например, в указанных на графике значениях в момент T = 0.04 частица 11 за время ΔTin = 3·10-4 сблизилась на минимальное расстояние Rmin = 2.5 с частицей Np = 6. Из рис. 8 по Np = 6 видно, какие еще были сближения частицы 11 с частицей 6. Аналогичными горизонтальными черточками или точками, расположенными по горизонтали, отображены номера частиц, с которыми сближалась частица 11. Номер центральной частицы 0 отображен на оси времени T на интервале 0.278 - 0.306.
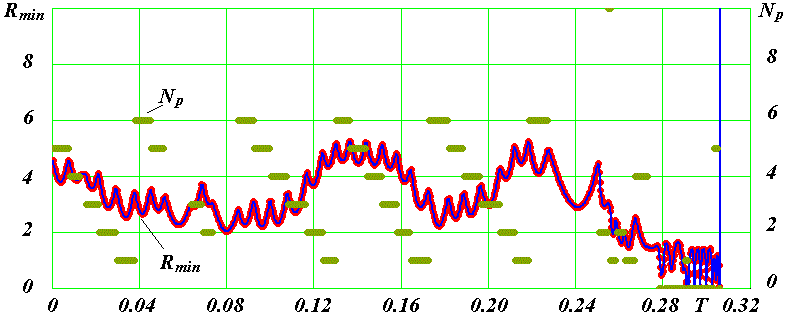
Рис. 8. Сближение частицы 11 за количество шагов интегрирования Kl3 = 3000 с шагом ΔT = 1·10-7 на минимальное расстояние Rmin с другими частицами, номера которых Np приведены числами на вертикальной оси.
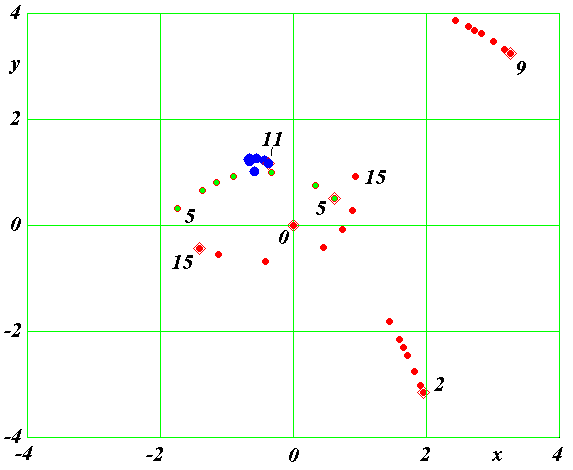
Рис. 9. Последовательные положения частиц с указанными номерами на плоскости xy на интервале времени T от 0.3035 до 0.3053. Начальные положения частиц отмечены ромбами, и движение происходит против часовой стрелки.
Перед выбросом частицы 11 из структуры решающим было ее сближение с частицей 5 (рис. 8). На рис. 9 показано движение частицы 11 в момент сближения с частицей 5. Здесь начальные положения частиц в момент T = 0.3035 отмечены ромбиками. Частица 11, как видно из рис. 6 и рис. 7b, движется по сильно вытянутой орбите. Она находится в апоцентрии, т.е. ее скорость движения небольшая. Орбита частицы 5 (рис. 9) не такая вытянутая, и к тому же она находится вблизи перицентрия. Поэтому скорость движения ее большая, и она догоняет частицу 11, проходя между ней и центральной частицей 0. Вследствие взаимного отталкивания происходит значительное уменьшение скорости частицы 11 (см. табл. 2).
Таблица 2. Изменение скорости v и расстояния r частицы 11 на интервале времени T от 0.3035 до 0.3053 при ее сближении с частицей 5.
| N точек | T | v | r |
| 1 | 0.3035 | 599.95 | 1.327 |
| 2 | 0.3037 | 419.85 | 1.416 |
| 3 | 0.3041 | 279.08 | 1.493 |
| 4 | 0.3045 | 141.00 | 1.521 |
| 5 | 0.3047 | 157.29 | 1.511 |
| 6 | 0.3049 | 315.08 | 1.467 |
| 7 | 0.3053 | 742.78 | 1.262 |
Как видно из табл. 2 безразмерная скорость частицы 11 в апоцентрии в результате ее взаимодействия с частицей 5 уменьшилась с 600 до 141, т.е. в 4.25 раза. Поэтому после ухода с ее пути частицы 5 начинается стремительное падение частицы 11 к центру.
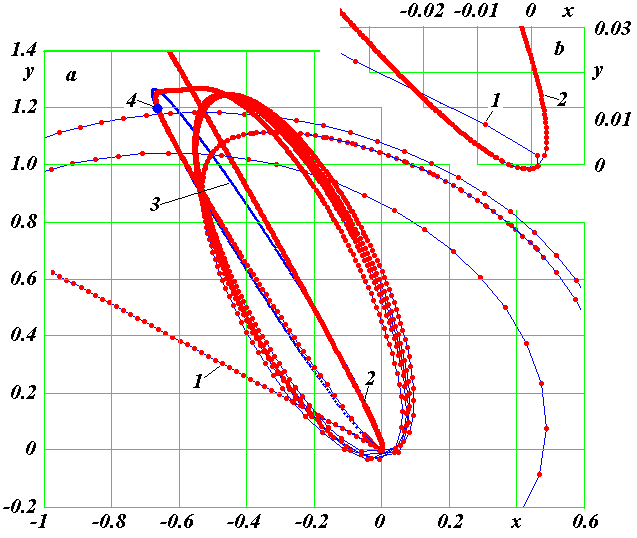
Рис. 10. Движение частицы 11 вокруг центральной частицы 0 на конечном участке траектории в обычном (a) и увеличенном (b) масштабах: 1 - при шаге счета ΔT = 1·10-7; 2 - после уточненных решений в момент сближения частицы 11 с частицей 0 с шагом счета ΔT = 1·10-8; 3 - движение частицы 11 в задаче двух тел с началом в точке 4 в момент T = 0.3048999. Точки на графиках соединены прямыми отрезками.
Этот участок движения частицы 11 в ее апоцентрии с характерным изломом траектории представлен на рис. 10а. Частица почти прямолинейно движется к центру с нарастающей скоростью. Она проходит на расстоянии r = 1.348·10-3 от частицы 0 и приобретает скорость v = 4.268·106. Затем частица 11 движется по прямолинейному участку траектории 1. Этот прямолинейный конечный участок траектории частицы 11 также представлен на рис. 6 - рис. 8. Рассмотрим его детальней.
В момент сближения частицы 11 с центральной тяжелой частицей 0 все остальные частицы находятся далеко и их влиянием на кинематический момент Mz,11 частицы 11 можно пренебречь. Поэтому можно считать, что общее изменение кинематического момента ΔMz всей структуры обусловлено погрешностью движения частицы 11. При сближении относительное изменение кинематического момента δMz всей структуры начинает увеличиваться. Когда абсолютные изменения момента ΔMz = δMz·Mz, где Mz = 0.6238, становятся сопоставимы с величиной кинетического момента частицы 11, то погрешности расчета ее движения возрастают пропорционально величине ΔMz.
До сближения частиц 11 и 0 величина δMz в программе Galactica имела порядок 10-14. Затем она начинает увеличиваться. Например, в момент T = 0.3060078 величины δMz = 2.35·10-9, ΔMz = 1.47·10-9, а величина момента частицы 11 Mz,11 = 7.47·10-4. Поэтому погрешность ее кинематического момента δMz,11 = ΔMz/Mz,11 = 1.96·10-6. Такую же величину относительной погрешности будут иметь координаты и скорости частицы 11. В этот момент частица 11 находится на расстоянии r = 0.019 от центральной частицы 0 и ее скорость v = 14939.
С дальнейшим приближением частицы 11 к центральной частице 0 величина δMz еще увеличивается и погрешность расчета движения частицы 11 становиться большой. Например, когда скорость частицы достигла величины v = 4.268·106 относительное изменение момента δMz = 0.36. Поэтому участок траектории с момента времени T = 0.29 был пересчитан с шагом ΔT = 0.5·10-7 в режиме автоматической коррекции шага. Отметим, что в программе Galactica коррекция шага производится по величине изменения δMz на нескольких шагах. В этом расчете частица 11 приблизилась к центральной частице 0 в момент T = 0.306008711 на расстояние r = 1.319·10-3 и скорость ее была v = 6.268·106. В этот момент относительная погрешность кинематического момента достигла δMz = 0.8. То есть с такой погрешностью получены эти результаты в точке сближения. Поэтому с момента T = 0.30600105 задача была пересчитана с шагом ΔT = 1·10-8. В этом случае в момент T = 0.30600871 частица 11 прошла у частицы 0 на расстоянии 1.30·10-3 и скорость ее по оценке была v = 6.1·104. Погрешность момента в этом случае δMz = 7.48·10-7. Эта величина дает для частицы 11 относительную погрешность момента ΔMz,11 = 6.03·10-4. Итак, с этой относительной погрешностью получены последние результаты. На рис. 11 уточненная траектория частицы 11 показана линией 2. По этой траектории частица выбрасывается из структуры.
Чтобы уточнить движение частицы 11 после сближения, участок траектории с момента T = 0.3048999 (см. точка 4 на рис. 10a) был еще пересчитан с шагом dT = 1·10-8 в режиме автоматической коррекции шага. Погрешность момента в этом случае была δMz = 7.78·10-7. Частица 11 сблизилась с частицей 0 на такое же расстояние 1.3·10-3 и скорость по оценке была v = 8.77·104. Траектория частицы 11 совпала с полученной в предыдущем расчете. Она показана на рис. 10a линией 2. На рис. 6 эта траектория за больший интервал времени приведена линией 11u. Скорость частицы уменьшается с ее удалением от центральной. К концу показанного участка траектории она достигает значение v = 1490. С этой скоростью частица выбрасывается из структуры.
Для сравнения были выполнены расчеты движения частицы 11 только под влиянием центральной частицы 0 , т.е. решалась задача двух тел. Как и в предыдущем расчете, начальной точкой была т. 4 на рис. 10 в момент T = 0.3048999. В этом случае частица 11 движется по эллиптической орбите 3 и не удаляется от центральной частицы 0 далее апоцентрия орбиты Ra = 1.539. В перицентрии с радиусом Rp = 2.081·10-3 частица достигает скорости v = 1.15·105. Эти результаты получены с погрешностью момента δMz = 1.03·10-5 и ΔMz = 1.0·10-8. В этом случае относительная погрешность момента частицы 11 δMz,11 = 1.34·10-5. С этой относительной погрешностью рассчитаны координаты и скорость частицы 11.
Итак, выполненные исследования показали, что в результате взаимодействий в структуре со многими частицами может происходить сближение одной из частиц с центральной частицей, а затем выброс этой частицы из структуры. В случае аналогичного взаимодействия двух частиц выброс частицы и разрушения двухчастичной структуры не происходит.
10. Второй вариант разрушения структуры
Решение вышерассмотренной задачи в этом режиме коррекции шага также приводит к разрушению структуры, но в этом случае из структуры выбрасывается частица 2. Рассмотрим этот вариант в той же последовательности, что и первый.
На рис. 11 показаны траектории центральной частицы 0 и двух первых частиц 1 и 2 первого слоя. Движение центральной частицы 0 за время T = 0.22, как показано линией II, происходит в области размером порядка 4·10-7. Область эта мала по сравнению с размером структуры. Частица 1 первого слоя из начального состояния, отмеченного точкой, совершает 7 обращений по траектории, которая слегка изменяется. Частица 2, как и частица 1 совершает 7 обращений практически без изменения (см. рис. 12). Затем она совершает два обращения по уменьшенной орбите (рис. 11 и рис. 12b) и переходит на вытянутую эллиптическую орбиту также меньшего размера. После совершения по ней 3-4 обращений частица 2 приближается к центральной частице 0, приобретает скорость vmax = 4.49·106 и затем выбрасывается из структуры.
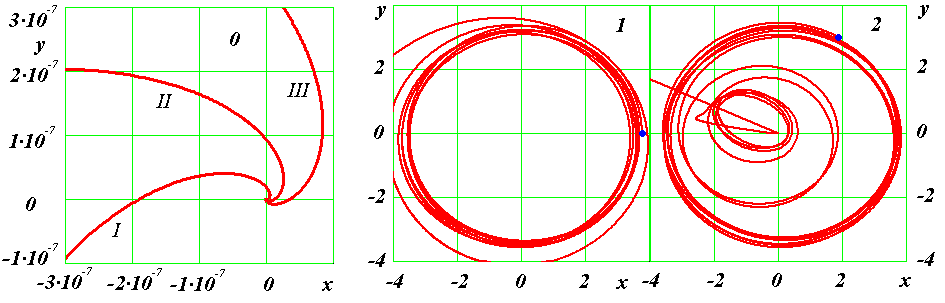
Рис. 11. Второй вариант траекторий трех частиц: центральной частицы 0 до момента T = 0.22; частиц 1 и 2 первого слоя до момента T = 0.294. I, II и III траектории частицы 0 в трех вариантах разрушения структуры.
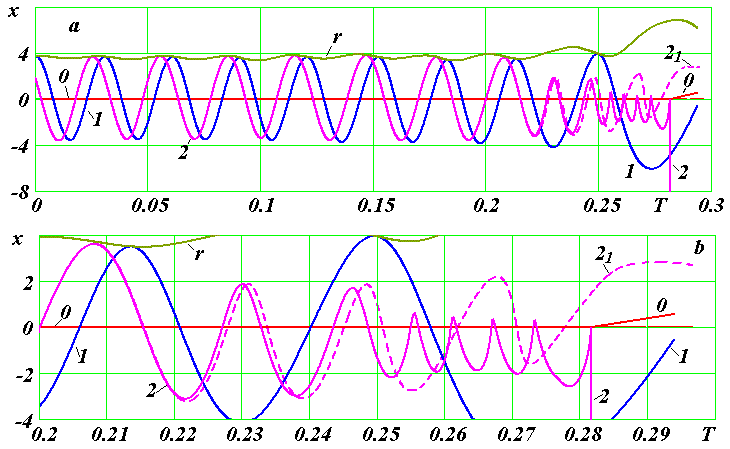
Рис. 12. Изменение во втором варианте координаты x во времени центральной частицы 0 и частиц 1 и 2 первого слоя, а также радиуса орбиты r частицы 1; 21 - закон движения частицы 2 в первом варианте: a - в обычном масштабе; b - в увеличенном масштабе.
Рассмотрим более детально движение частицы 2 после семи ее обращений по устойчивой орбите. В момент T = 0.22279 частица 2 сблизилась с частицей 3 на расстояние r = 1.99284 (см. рис. 13). После этого сближения она сошла с устойчивой орбиты (см. рис. 12), и в момент T = 0.2300902 сблизилась с центральной частицей 0 (см. рис. 13) на расстояние r = 1.8734. После совершения двух обращений по уменьшенной орбите (рис. 12) в момент T = 0.25003375 произошло сближение частицы 2 с частицей 5 (рис. 13) на расстояние r = 1.011, в результате которого частица перешла на уменьшенную орбиту (рис. 12). После совершения трех обращений частица 2 в момент T = 0.2769445 сближается с частицей 12 (рис. 13) на расстояние r = 0.369, в результате которого она теряет скорость и падает к центру, приближаясь на расстояние r = 8.76·10-4 и приобретая скорость vmax = 4.49·106.
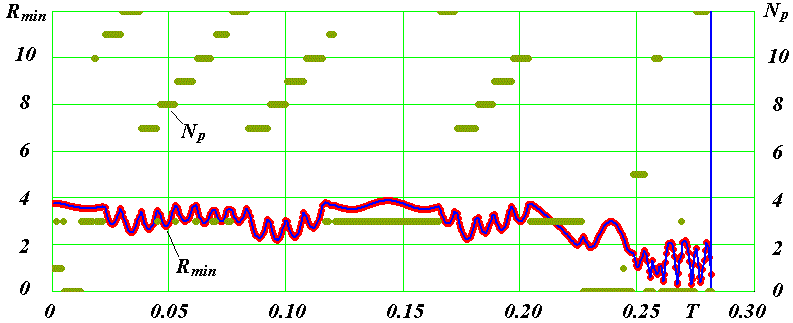
Рис. 13. Сближение частицы во втором варианте 2 за количество шагов интегрирования Kl3 = 5000 (при переменном шаге) на минимальное расстояние Rmin с другими частицами, номера которых Np приведены числами на вертикальной оси.
Во всех случаях сближения частицы 2 с одноименно заряженными частицами 3, 5, 12 происходит ее торможение, поэтому скорость частицы 2 уменьшается, и орбита ее приближается к центральной частице. Более детально процесс взаимодействия частиц 2 и 12 виден на рис. 14. Как и частица 11 в первом варианте, частица 2 находится в апоцентрии своей орбиты. Поэтому ее скорость мала. Частица 12 в этот момент находится вблизи своего перицентрия, и скорость ее значительно больше. Поэтому она догоняет частицу 2, и, проходя между ней и центром 0, отталкивает ее от центра. Таким образом, частица 2 теряет свою скорость. Как видно из табл. 3 скорость ее падает почти в 7 раз. После чего начинается ее стремительное движение к центральной частице 0 (рис. 15). Она проходит, как уже отмечалось, на расстоянии r = 8.76·10-4, достигает скорости v = 4.49·106 и выбрасывается из структуры. В рассматриваемом случае частица 2 ближе по сравнению с первым случаем подходит к ядру 0, поэтому ее скорость больше. Следует отметить, что при уточнении расчета участка сближения величины r и v будут несколько отличаться.
Рис. 14. Последовательные положения частиц с указанными номерами на плоскости xy на интервале времени T от 0.27542685 до 0.2799259. Начальные положения частиц отмечены ромбами. Вариант 2. |
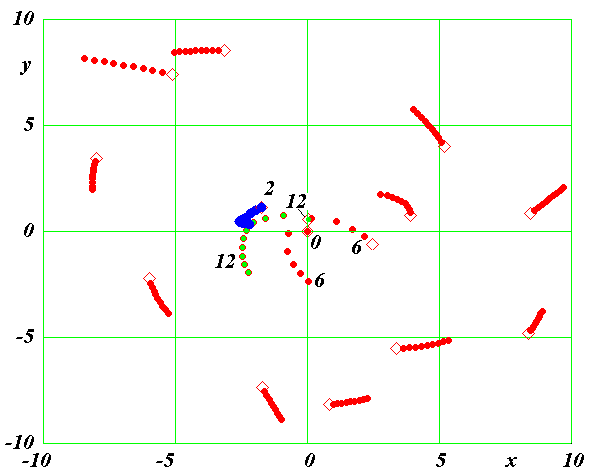 |
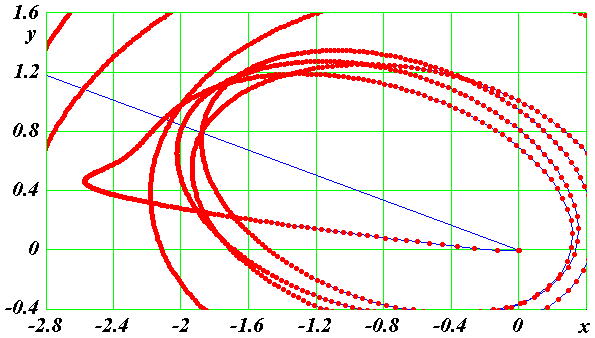
Рис. 15. Движение частицы 2 по ее орбите с наименьшим радиусом и вокруг центральной частицы 0 в момент выброса из структуры.
Таблица 3. Изменение скорости v и расстояния r частицы 2 на интервале времени T от 0.27542685 до 0.2799259. В таблице числа для T дополняют величину 0.27.
| N точек | T, 0.27… | v | r |
| 1 | 54268501 | 605.1 | 2.128 |
| 2 | 592675 | 518.7 | 2.260 |
| 3 | 642660 | 487.7 | 2.336 |
| 4 | 692655 | 442.1 | 2.408 |
| 5 | 742640 | 256.9 | 2.521 |
| 6 | 792625 | 159.4 | 2.602 |
| 7 | 842610 | 86.47 | 2.622 |
| 8 | 892610 | 182.96 | 2.572 |
| 9 | 942605 | 336.07 | 2.447 |
| 10 | 992590 | 520.91 | 2.236 |
Как в первом, так и во втором случае, сход частицы 11 и частицы 2 со своих устойчивых орбит обусловлен последовательными сближениями с одноименно заряженными частицами. В каждом таком сближении рассматриваемая частица теряет скорость и переходит на орбиту с меньшим радиусом. В обоих случаях частицы совершают по три перехода. В рассмотренных двух случаях на последнем этапе сильное торможение частиц со снижением скорости в несколько раз происходит одинаково. Частица, находясь в апоцентрии сильно вытянутой орбиты, имеет малую скорость. В этот момент между ней и притягивающим центром проходит частица, которая своим кулоновским отталкиванием осуществляет это торможение. После этого частица почти радиально движется к центру и в перицентрии своей траектории приобретает такую скорость, которая приводит к выбросу ее из структуры.
11. Анализ различий в двух вариантах динамики частицы 2
Получены два варианта разрушения четырехслойной структуры. В первом варианте частица 11 после сближения с частицей 5 в момент T = 0.3045 тормозится, после чего сближается с центральной частицей 0, приобретает большую скорость и выбрасывается из структуры. Во втором варианте аналогичный процесс происходит с частицей 2 после ее сближения в момент T = 0.27694545 с частицей 12. Так как последнее событие происходит раньше предыдущего, возникает вопрос: почему оно не произошло в первом варианте?
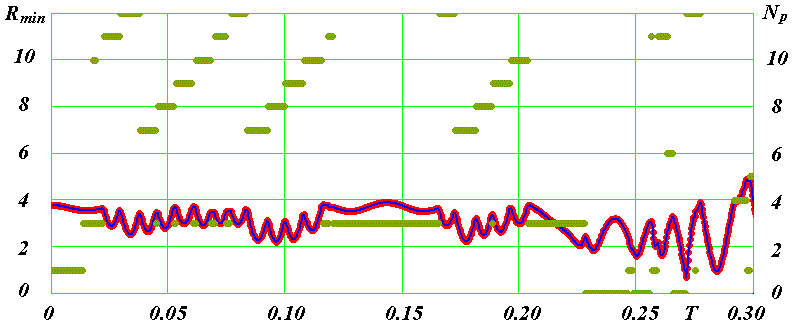
Рис. 16. Сближение частицы 2 в первом варианте за количество шагов интегрирования Kl3 = 5000 (при шаге ΔT = 10-7) на минимальное расстояние Rmin с другими частицами, номера Np которых приведены числами на вертикальной оси.
Чтобы ответить на этот вопрос, рассмотрим на рис. 16 историю сближения частицы 2 с другими частицами в первом варианте. Из сопоставления с данными рис. 13 следует, что до момента T = 0.2439344 она практически совпадает с историей сближения частицы 2 во втором варианте. В этот момент во втором варианте (рис. 13) частица 2 сближается с частицей 5. Затем следуют еще 10 сближений с ней, после которых истории сближений частицы 2 начинают существенно отличаться.
В более крупном масштабе истории сближений частицы 2 в двух вариантах сопоставлены на рис. 17 на интервале времени T от 0.2 до 0.25. В этом масштабе видно, что количественные отличия зависимостей Rmin(T) для двух случаев начинают наблюдаться с T = 0.2. К моменту T = 0.2439344 они увеличиваются настолько, что взаимодействие частицы 2 с частицей 5 приводит к качественным изменениям движения частицы 2. Итак, причина качественных изменений движения частицы 2 заключается в увеличении со временем небольших количественных изменений ее движения.
Рассмотрим, как они появляются в начальный момент T = 0. Из сравнения рис. 13 и рис. 16 видны отличия в сближении частицы 2 с соседними частицами 1 и 3 своего слоя. Как видно из рис. 4, частица 2 находится на одинаковом расстоянии от частиц 1 и 3: частица 3 расположена впереди частицы 2, а частица 1 - сзади. В первом варианте (рис. 16) в начальный момент (T ~ 0) частица 2 сближается с задней частицей 1. Так как частицы взаимно отталкиваются, то задняя частица ее ускоряет. Во втором варианте (рис. 13) сближения частицы 2 с частицей 1 прерываются двумя сближениями с передней частицей 3, которая замедляет частицу 2. Вследствие уменьшения скорости частицы 2 появляются ее сближения с центральной частицей 0. Величины изменений скорости очень малы, но т.к. вначале расстояния частицы 2 от центральной 0 и частиц 1 и 3 одинаковы, влияние изменений скорости на координаты частицы хорошо прослеживается на графиках сближений.
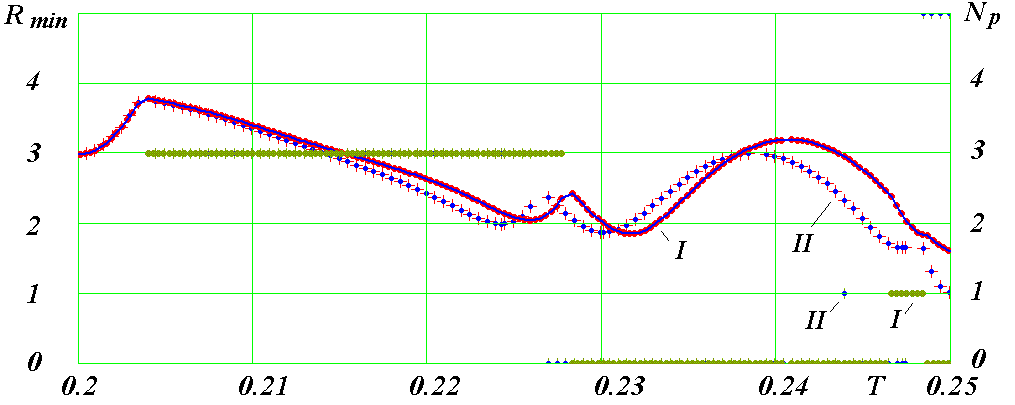
Рис. 17. Сравнение историй сближения частицы 2 в двух вариантах: I - первый вариант; II - второй вариант.
Изменение порядка сближений частицы 2 с частицами 1 и 3 обусловлено изменениями вычислительного процесса во втором варианте. В это время во втором варианте было несколько переходов с шага ΔT = 1·10-7 на шаг ΔT = 0.5·10-7. Переход на другой шаг приводит к тому, что значения характеристик взаимодействия, например, расстояния между частицей 2 и соседними частицами 1 и 3 изменяются. При первоначальном одинаковом положении частицы 2 между частицами 1 и 3, небольшие изменения приводят к сближению к одной из частиц. Если частица 2 сближается с передней 3, то она тормозится, а если с задней 1 - то ускоряется. При анализе траектории частицы эти явления и наблюдаются.
При рассмотрении сближений Rmin(T) за меньшее число шагов Kl3 видно, что частица 2 во втором варианте больше сближалась с передней частицей 3, нежели с задней частицей 1. Поэтому во втором варианте частица 2 больше потеряла скорость. При потере скорости частица приближается к центру притяжения. По этой причине, как уже отмечалось, появились ее сближения с центральной частицей 0 (рис. 13).
Вернемся к конечному участку движения частицы 2 (см. рис. 17). До T = 0.21 величины Rmin для двух вариантов неотличимы. Со временем различия увеличиваются, при этом минимумы и максимумы Rmin во втором варианте наступают раньше, т.е. опережают экстремумы Rmin в первом варианте. Опережение обусловлено тем, что угловая скорость обращения частицы 2 относительно центральной частицы увеличилась. Увеличение угловой скорости происходит из-за уменьшения радиуса орбиты. А радиус орбиты частицы 2 уменьшился во втором варианте за счет торможения ее передней частицей 3 при большем количестве приближений к последней. Итак, более сильное взаимодействие частицы 2 с частицей 3 во втором варианте привели к большей ее скорости обращения по своей орбите по сравнению с первым вариантом.
На рис. 12 линией 21 приведена траектория частицы 2 в I-ом варианте. Видно, что экстремумы частицы 2 во втором варианте также наступают раньше. Итак, частица 2 (рис. 17) вследствие более быстрого обращения по своей орбите в момент T = 0.2484334 минует сближения с частицей 5 и не переходит на орбиту с меньшим радиусом. Поэтому в первом варианте при дальнейшем движении не происходят события, которые приводят к выбросу частицы 2 из структуры.
Рассмотрим более детально начальные изменения в траектории частицы 2 в варианте II по сравнению с вариантом I. На рис. 18 показано относительное изменение координаты частицы xII во втором варианте по сравнению с ее координатой xI в первом варианте:
| δx = (xII - xI)/r, | (39) |
где r - радиус траектории частицы 2.
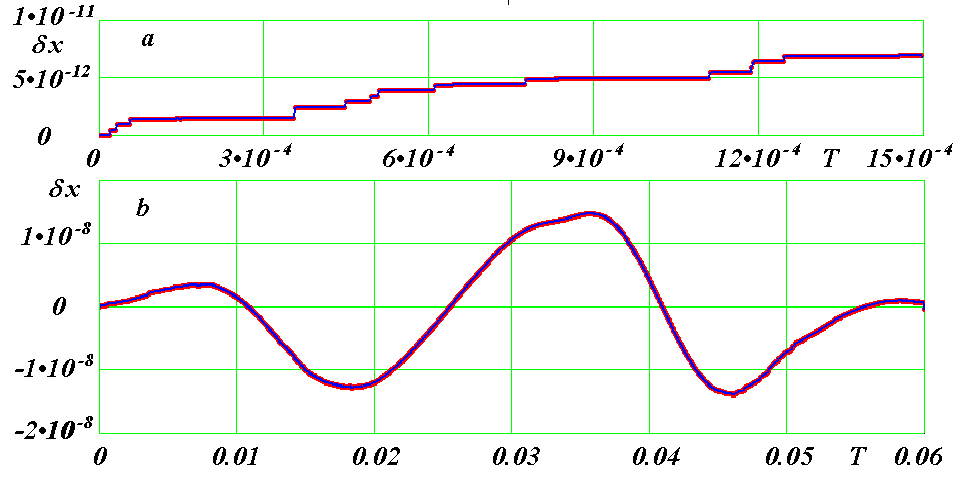
Рис. 18. Динамика относительного изменения координаты x частицы 2 во втором варианте по сравнению с первым: a - до T = 0.0015; b - за время T = 0.06.
Как видно из рис. 18a до T = 0.0015 величина δx изменяется ступенчато. Каждая ступенька вызвана переходом на меньший шаг ΔT = 0.5·10-7. Первое изменение δx = 5·10-13. Это значение имеет порядок величины единицы последнего разряда координаты x, которая выражена числами двойной длины. То есть переход на другой шаг вызывает изменения в результатах интегрирования в последнем разряде чисел.
Каждая ступенька на рис. 18a совпадает с переходом на шаг ΔT = 0.5·10-7, после счета с которым происходит возврат к шагу ΔT = 1·10-7. До T = 0.008 величина δx растет линейно со временем, затем она колеблется с амплитудой 1.5·10-8 (см. рис. 18b). Эти колебания обусловлены колебаниями координаты x из-за запаздывания экстремумов xII относительно экстремумов xI.
Отличия в последнем разряде чисел при изменении параметров вычислительного процесса имеются всегда. Если вычислительный метод и задача устойчивы, то конечные результаты интегрирования уравнений остаются практически неизменными. В данном случае неизменным является разрушение структуры: оно проходит после 7-ого оборота внутреннего слоя, и движение частиц, как видно из кривых 2 и 21 на рис. 12, до T = 0.24 практически не изменяется. В данном случае структура неустойчива. Поэтому ее разрушение происходит разными способами. По-видимому, способов разрушения может быть столько, сколько будет отличий вычислительного процесса.
12. Третий вариант разрушения структуры
В этом варианте задача решалась с постоянным шагом ΔT = 0.5·10-7. В этом случае в момент T = 0.269 из структуры выбрасывается частица 7, которая является первой частицей второго слоя (рис. 4). На рис. 19 приведены траектории частиц за время T = 0.371: 0 - центральной, 1 - первой частицы первого слоя и 7 - первой частицы второго слоя. За время T = 0.21 движение центральной частицы 0 происходит циклически с возрастающим радиусом траектории. Траектория центральной частицы 0 за время T = 0.21 показана на рис. 11 в сравнении с ее траекторией в других вариантах. Как видно размеры области движения частиц одинаковы. Отличие заключается в разных углах разворота. Они обусловлены тем, что первоначальное положение выбрасываемых в этих вариантах частиц 11, 2 и 7 определяется разными углами и радиусами. Поэтому изменение их движений по разному отражается на смещении центральной частицы.
До разрушения структуры частица совершает 7 обращений по практически неизменной орбите, а после разрушения структуры движется по эллиптической орбите с увеличенным радиусом. Затем уходит на орбиту с еще большим радиусом.
Траектория частицы 7 на первых двух обращениях подобна траектории частицы 11 того же слоя в варианте I на рис. 6. Отличие заключается в том, что траектория повернута на тот угол, на который повернуто начальное положение частицы 7 относительно частицы 11. Как и частица 11, частица 7 (рис. 19) совершает два обращения по эллиптической орбите. Затем непрерывно переходит на орбиты меньшего радиуса и после сближения с центральной частицей 0 выбрасывается из структуры.
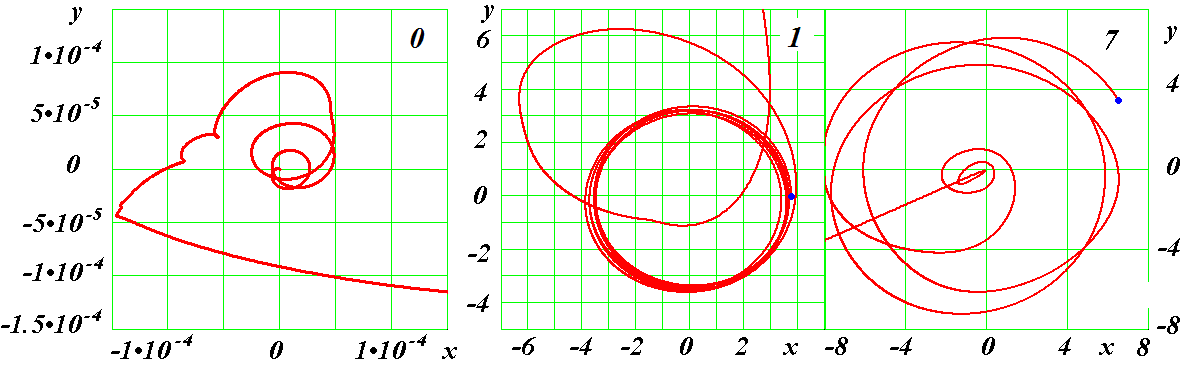
Рис. 19. Третий вариант траекторий трех частиц: центральной частицы 0 до момента T = 0.2759; частицы 1 первого слоя и частицы 7 второго слоя до момента T = 0.371.
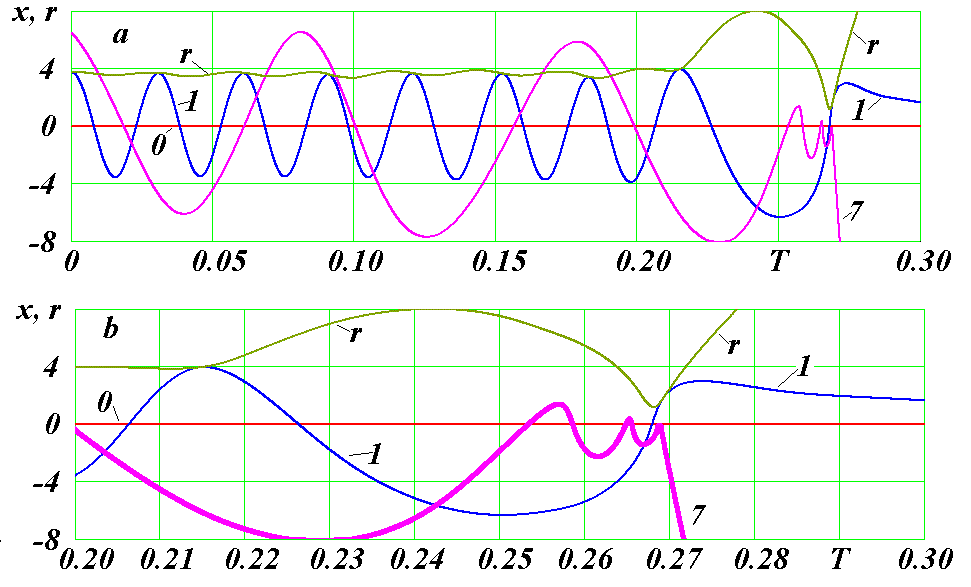
Рис. 20. Изменение в третьем варианте координаты x во времени центральной частицы 0 и частиц 1 и 7, а также радиуса орбиты r частицы 1: a - в обычном масштабе; b - в увеличенном масштабе.
Законы движения x(T) этих двух частиц показаны на рис. 20. До T = 0.22 они идентичны законам движения частиц на рис. 7. Затем частица 7 переходит на орбиты с уменьшающимся радиусом (рис. 20b) и в момент T = 0.269 после сближения с центральной частицей (x = 0) выбрасывается из структуры. По изменению радиуса r видно, что в этот момент частица 1 приближается к центру, а затем удаляется от него.
Картина сближений частицы 7 с другими частицами показана на рис. 21. Вначале частица 7 находится вблизи частицы 1. Затем ее движение проходит поблизости от частиц 6 и 14. До момента T = 0.2267 сближение частицы 7 с частицами 1, 2, 3, 4, 5 и 6 циклически повторяются. После ее сближения с частицей 5 в момент T = 0.24848855 частица 7 уменьшает радиус своей орбиты, и, как видно из рис. 21b, после взаимодействий с частицами 6, 8, 7 и 0 ее расстояние к центральной частице 0 уменьшается. В момент T = 0.2647866 частица 7 сближается с частицей 8 на расстояние r = 0.287, которая тормозит ее. После чего частица 7 сближается с центральной частицей 0. Затем в момент T = 0.26770775 она сближается с частицей 1 на расстояние r = 0.2456, в результате чего обе частицы тормозятся и резко изменяют траектории (см. рис. 20b). После этого частица 7, как следует из данных рис. 21, в момент T = 0.2686336 приближается к частице 0 на расстояние 2.66·10-3 и совершает один оборот по вытянутой эллиптической траектории с радиусом апоцентрия 0.356 (см. рис. 22). Затем в момент T = 0.2689333 сближается с центральной частицей на расстояние r = 2.47·10-3 и выбрасывается из структуры. При этом частица 7 приобретает скорость при первом сближении 28500, а при втором - 33600. Последняя скорость быстро уменьшается с удалением частицы 7 от центра и к моменту T = 0.371 скорость равна 3058. С этой скоростью частица 7 выбрасывается из структуры. Как видно из рис. 21, при выходе из структуры она проходит вблизи частиц 17 и 21. Следует отметить, что излом траектории центральной частицы 0 на рис. 19 происходит в момент выброса частицы 7.
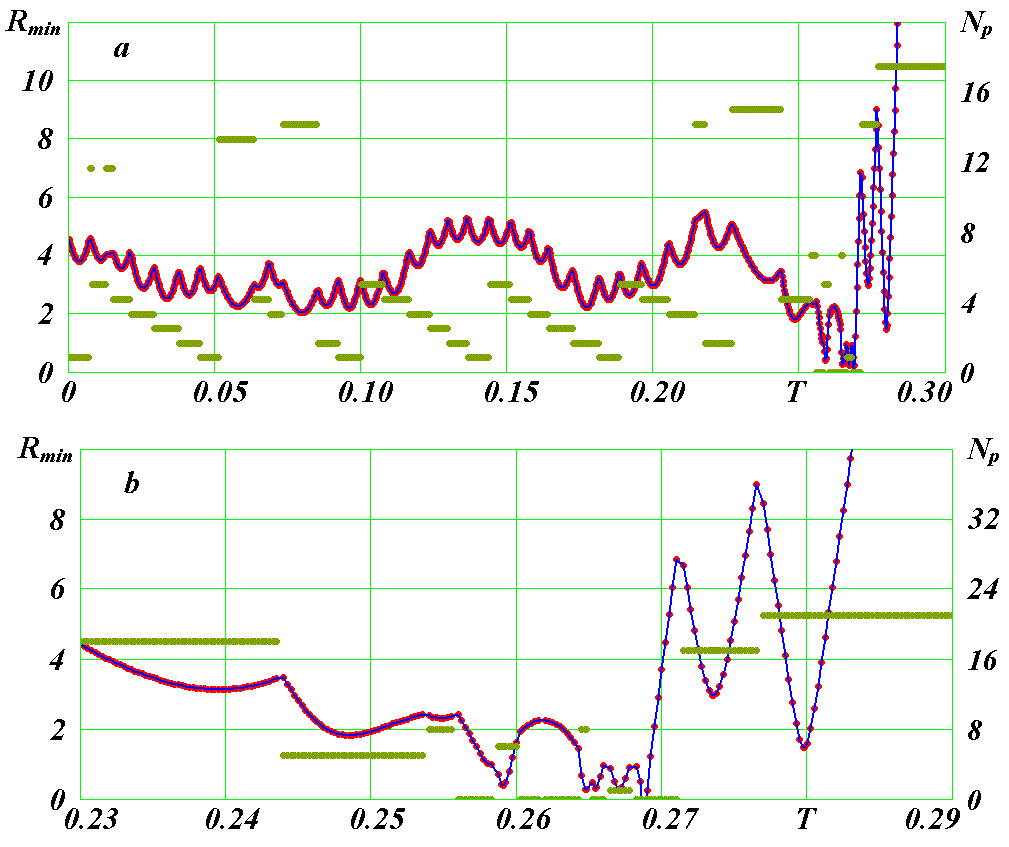
Рис. 21. Сближение частицы 7 в третьем варианте за количество шагов интегрирования Kl3 = 5000 (при шаге ΔT = 0.5?10-7) на минимальное расстояние Rmin с другими частицами, номера Np которых приведены числами на вертикальной оси: a - в обычном масштабе; b - в увеличенном масштабе.
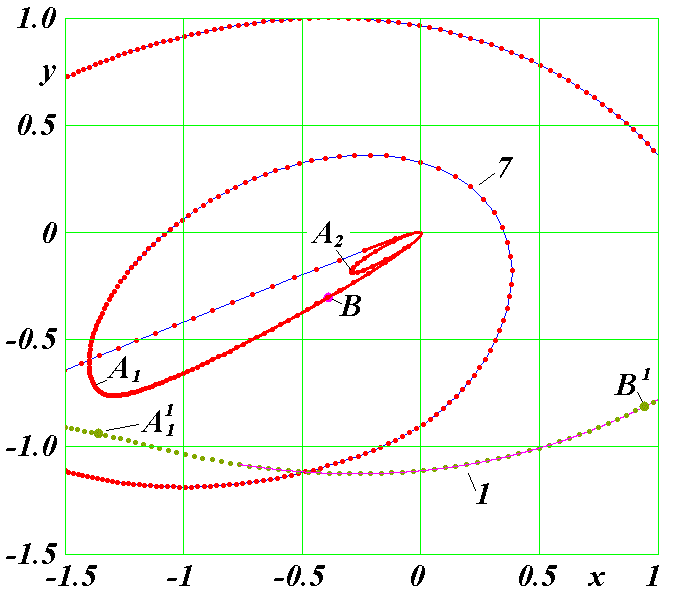
Рис. 22. Движение частицы 7 в третьем варианте по ее орбите вокруг центральной частицы 0 в момент выброса из структуры. 1 - траектория первой частицы; A1 и A11, B и B1 - одновременные точки на траекториях частиц 7 и 1, соответственно.
На рис. 22 показано, что изменения в движении частицы 7 обусловлены взаимодействием ее с частицей 1. В апоцентрии своей орбиты (т. А1) частица 7 в момент T = 0.267770775 она сближается с частицей 1 на расстояние r = 0.2456 и тормозится. Поэтому устремляется к центру и в момент T = 0.2686336 достигает своего перицентрия. Затем движется по эллиптической орбите в направлении частицы 1 и снова тормозится. Во втором апоцентрии (т. A2) частица с уменьшенной скоростью снова движется к центру, проходит ближе к нему. Поэтому приобретает большую скорость. Увеличению ее скорости на этом участке после т. A2 способствует также отталкивание частицы 1. Благодаря такому воздействию этой частицы частица 7 выбрасывается из структуры.
13. Уникальные события в варианте III
Рис. 23. Траектория частицы 4 в третьем варианте до момента T = 0.370729255 ее столкновения с центральной частицей. С начального положения, отмеченного точкой, частица 4 обращается против часовой стрелки, а с положения C - за часовой стрелкой.
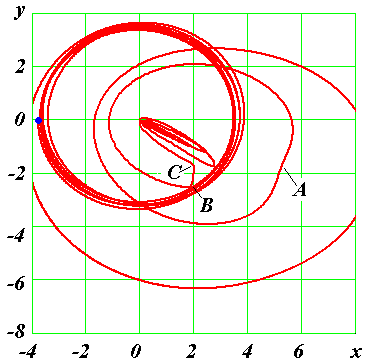
После разрушения структуры в ней происходят два уникальных события: частица 4 изменяет направление своего обращения и в момент T = 0.370729255. сталкивается с центральной частицей. Рассмотрим движение частицы 4 более детально. Ее траектория представлена на рис. 23. Напомним, что в этом варианте движения частиц 0, 1 и 7 показано на рис. 19. Частица 4 первого слоя (рис. 23), также как и частица 1, совершает 7 обращений по практически неизменной траектории, затем уходит на орбиту с большим радиусом. По этой орбите частица 4, не завершив полного обращения, начинает приближаться к центру, обращаясь вокруг него по уменьшающейся орбите. На траектории частицы 4 видны изломы A, B и C, обусловленные сближениями с частицами. После одного из таких изломов B частица меняет свое направление обращения вокруг центральной частицы. Первоначальное ее движение происходит против часовой стрелки, а в конце частицей 4 совершены обращения по часовой стрелке.
|
Рис. 24. Изменение в третьем варианте координаты x во времени центральной частицы 0 и частиц 1 и 4, а также радиуса орбиты r частицы 1: a - в обычном масштабе; b - в увеличенном масштабе.
Закон движения x(T) частицы 4 показан на рис. 24. Ее обращения вокруг центральной частицы по орбитам с большим радиусом видны на рис. 24a, а с малыми радиусами - на рис. 24b. На последнем участке частица делает 6 обращений на орбитах с малым радиусом, причем апоцентрии орбиты увеличиваются. И на последнем обращении в момент T = 0.370729255 частица 4 достигает радиуса r = 4.94·10-4, который равен сумме радиусов частиц 4 и 0, т.е. происходит столкновение этих частиц.
История сближений частицы 4 с другими частицами представлена на рис. 25. После разрушения структур происходит ее сближение с частицей 3 в момент T = 0.21524945 на расстояние r = 1.77. Так как частица 3 находится сзади, то это сближение привело к ускорению частицы 4 и переходу на орбиту с большим радиусом (рис. 24).
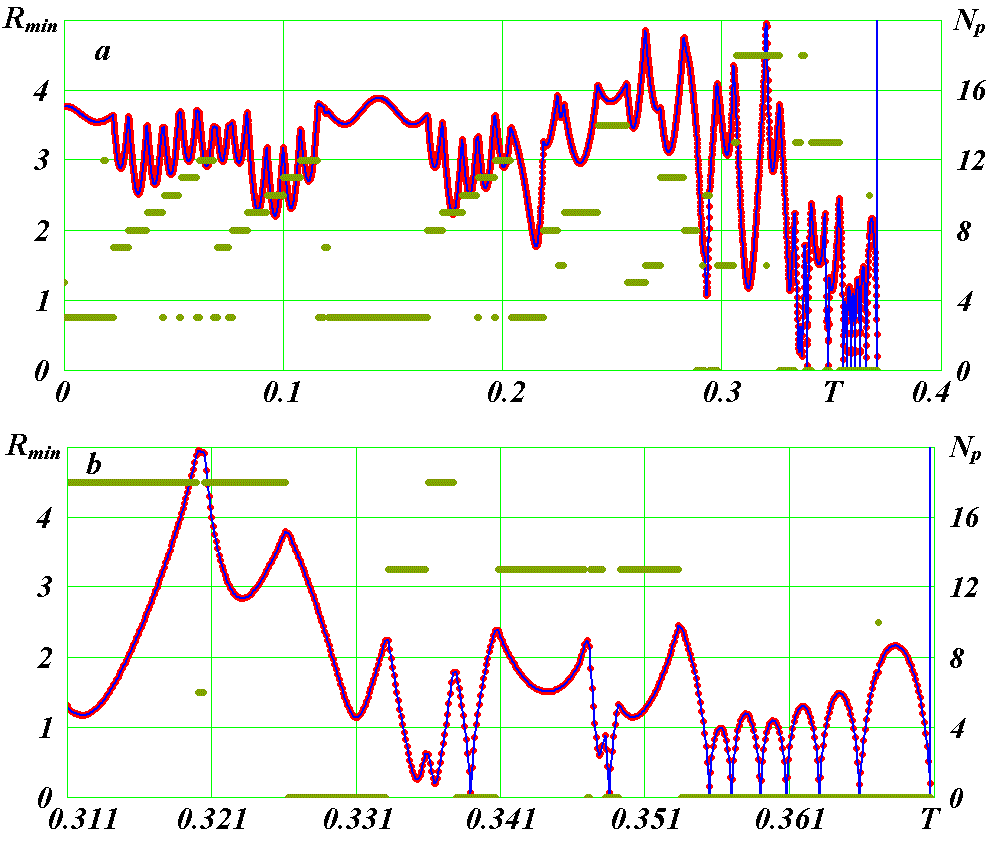
Рис. 25. Сближение частицы 4 в третьем варианте за количество шагов интегрирования Kl3 = 5000 (при шаге ΔT = 0.5·10-7) на минимальное расстояние Rmin с другими частицами, номера Np которых приведены числами на вертикальной оси: a - в обычном масштабе; b - в увеличенном масштабе.
В момент T = 0.2930048 после того, как частица 4 прошла перицентрий, происходит ее сближение с частицей 10 на расстояние r = 1.074. Это сближение, а также предшествующие сближения с частицей 6 привело к торможению частицы 4. Поэтому она уходит с орбиты с большим апоцентрием (рис. 23).
В момент T = 0.31202265 (рис. 25b) произошло сближение частицы 4 с частицей 18 на расстояние r = 1.17, которое отразилось в изменении траектории в т. А (рис. 23). В момент T = 0.33519475 частица 4 сближается (рис. 25b) с частицей 13 на расстояние r = 0.253, а в момент T = 0.336446 она сближается с частицей 18 на расстояние r = 0.195. Эти тесные сближения привели к изломам траектории B и C на рис. 23. После этих изломов частица 4 начала обращаться вокруг центральной частицы по часовой стрелке. На дальнейшее движение частицы 4, как видно из 25b, продолжала оказывать влияние частица 13 до момента T = 0.347837, после которого в момент T = 0.348507 частица 4 сближалась с центральной частицей 0 на расстояние r = 1.52·10-2. После этого еще до момента T = 0.353 частица 13 продолжала тормозить частицу 4. Дальнейшее движение частицы 4 вокруг частицы 0 происходило без преимущественного влияния какой-либо из частиц. И только на последнем обращении влияние оказала частица 10. Все предыдущие 5 обращений проходили при достижении радиуса перицентрия в пределах от 0.275·10-3 до 2.79·10-3. А на последнем обращении, в момент сближения, радиус перицентрия уменьшился более чем в 5 раз и достиг значения r = 4.94·10-4. При столкновении с центральной частицей скорость частицы 4 достигает значения v = 92826.
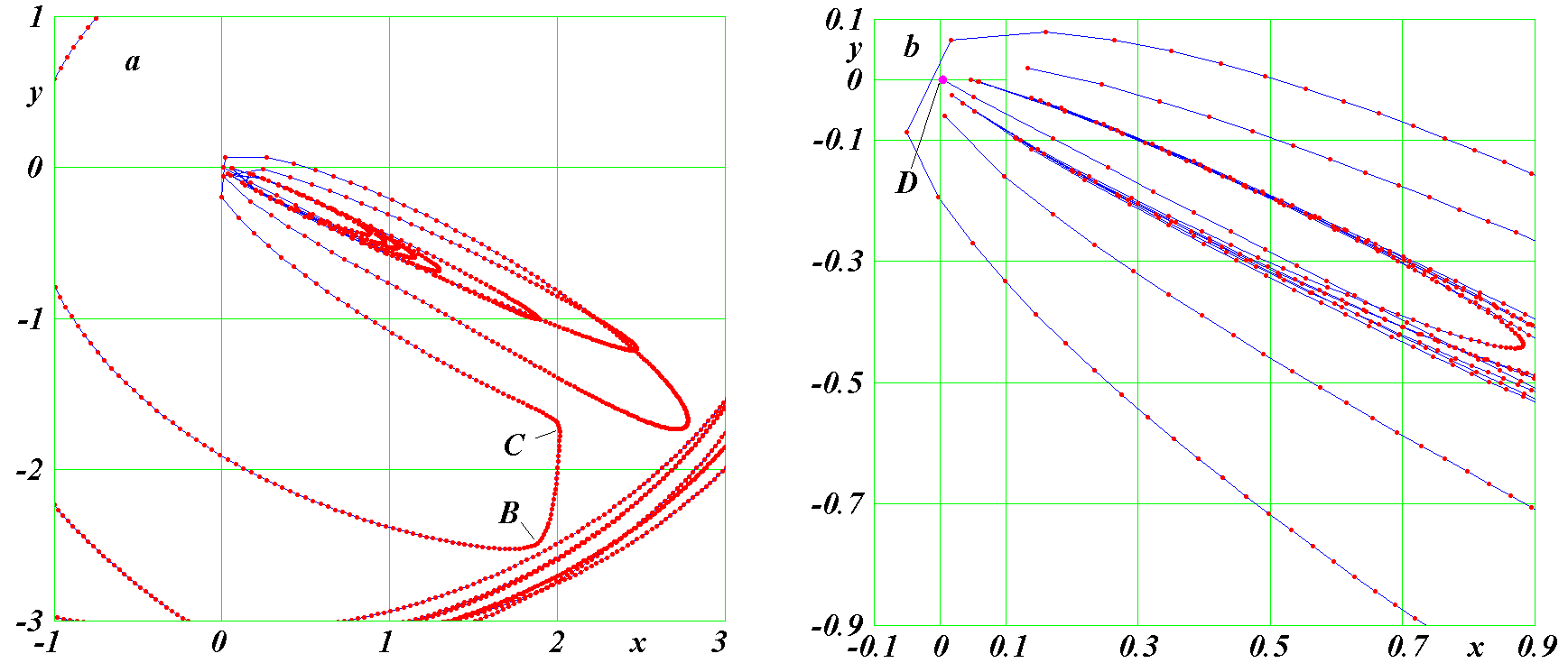
Рис. 26. Движение частицы 4 в третьем варианте по ее траектории вокруг центральной частицы в момент столкновения с ней: a - в обычном масштабе; b - в увеличенном масштабе.
На рис. 24b, начиная с момента T = 0.338915452 видны 9 сближений частицы 4 с центральной частицей 0. Они происходят при восьми обращениях частицы 4 вокруг последней. На рис. 26a эти обращения следуют после т. C, т.е. они, как уже отмечалось, происходят по часовой стрелке. На рис. 26 b эти обращения показаны в увеличенном масштабе. Точкой D отмечено положение частицы 4 в момент ее столкновения с центральной частицей 0.
14. Динамика других структур
На рис. 27 представлена двухслойная структура с N3 = 12, kr = 1, Prdi = 3.29471·10-17 c. Ее вид не изменяется до момента T = 0.1 на протяжении трех оборотов внутреннего слоя. Затем круговая орбита частиц внутреннего слоя начинает нарушаться. Попарно противоположные частицы имеют одинаковые изменения орбиты. Эти изменения нарастают, пока кольцо не распадаются на ряд колец, с двумя частицами на каждом см. рис. 28.
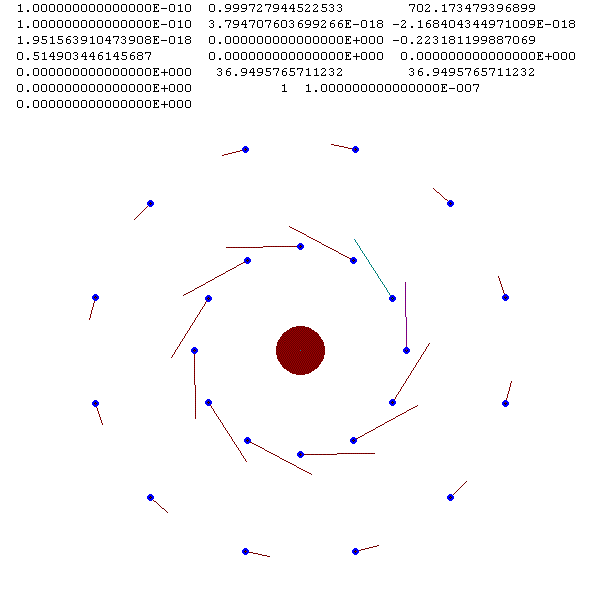
Рис. 27. Вид двухслойной структуры с N2 = 2 и N3 = 12.
В этих кольцах строгая симметрия частиц отсутствует. Поэтому в течение непродолжительного времени начинаются сближения частиц, что приводит к окончательному разрушению структуры.
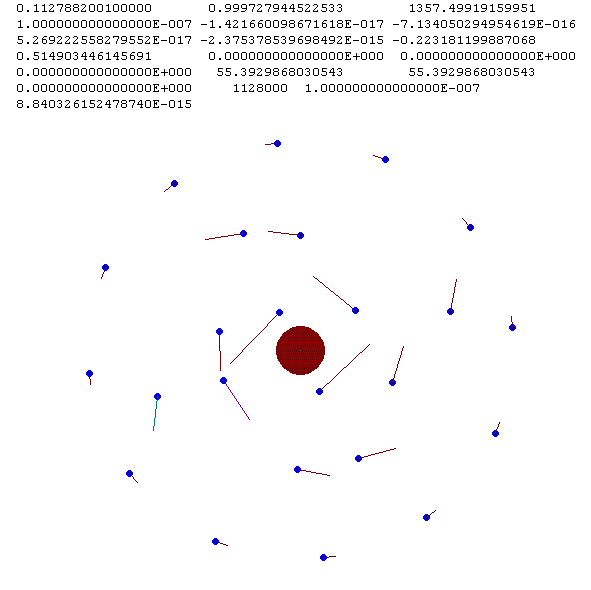
Рис. 28. Начало разрушения двухслойной структуры при T = 0.1128.
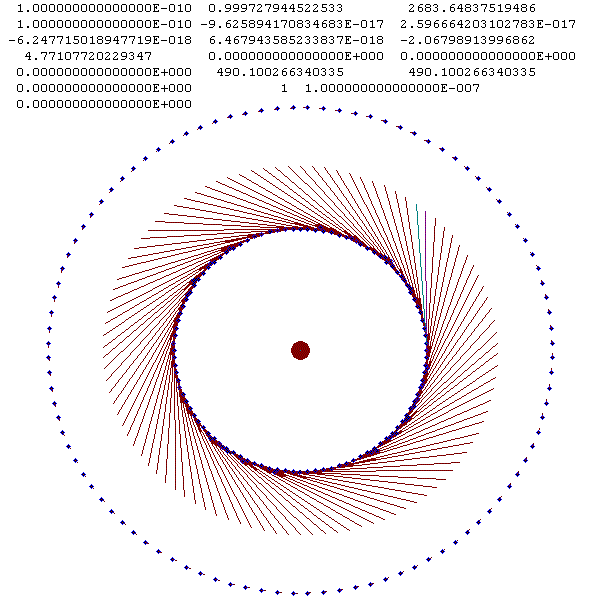
Рис. 29. Вид двухслойной структуры с N2 = 2, N3 = 100, kr = 1 и Prdi = 3.29471·10-17 c.
На рис. 29 показана двухслойная структура с N3 = 100. Ее вид не изменяется до момента T = 0.013, что соответствует полуобороту внутреннего слоя. Затем внутренний слой распадается на два близких кольца. В результате взаимных сближений частиц происходит распад этих колец.
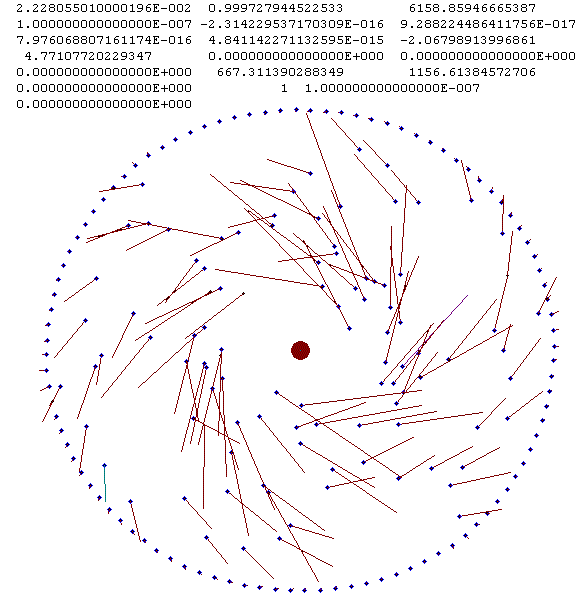
Рис. 30. Начало разрушения двухслойной структуры при T = 0.0223.
Частицы заполняют все пространство наружного кольца (см. рис. 30). При их сближении с частицами этого же кольца, у последних увеличиваются радиальные составляющие скорости. Сближение отмеченных частиц приводит к быстрому разрушению наружного слоя.
На рис. 31 показана комбинированная трехслойная структура, которая математически составлена из пяти колец: N2 = 5 и N3 = 8. Как отличалось ранее, она имеет попарно одинаковые радиусы у колец 2 и 3, 4 и 5. Так как углы j,1 у колец с одинаковыми радиусами отличаются, то и суммарные силы, воздействующие на частицы на кольцах, отличаются. Это приводит к отличию периодов обращения частиц, находящихся в одном слое. Так периоды обращения частиц во втором слое отличаются в третьем знаке, а в третьем слое - в шестом.
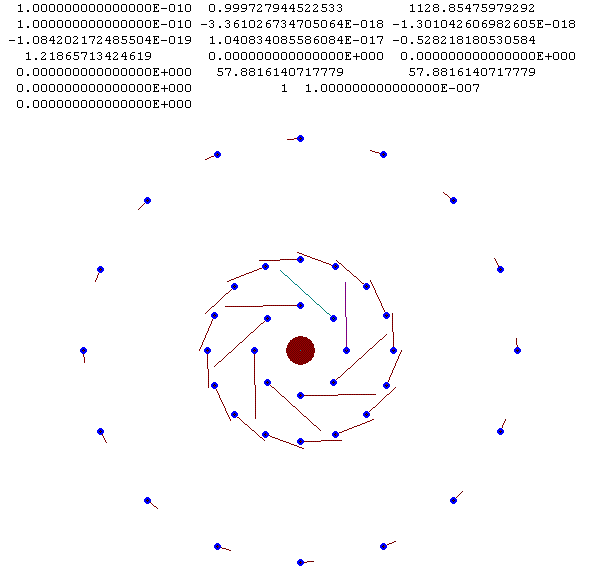
Рис. 31. Комбинированная трехслойная структура с N2 = 5 и N3 = 8 и Prdi = 3.29471·10-17 c. Относительные радиусы пяти колец: = 2.8, 5.6, 5.6, 13.0, 13.0.
До момента T = 0.0245, соответствующему одному обороту внутреннего слоя, структура не изменяется. Затем второе кольцо начинает расслаиваться и в момент T = 0.0493 из него образуется два слоя по 8 частиц в каждом. Один из них, назовем его вторым слоем, приближается к первому слою, а радиус второго кольца, назовем его третьим слоем, увеличивает в 1.28 раза. К моменту T = 0.0973 третий слой приближается к наружному слою и из последнего начинает выделяться пятый слой, содержащий 8 частиц. На рис. 32 все пять слоев по восемь частиц в каждом показаны в момент T = 0.12. До этого момента третий слой достиг наибольшего своего размера, начал сжиматься и приблизился к внутренним слоям.

Рис. 32. Расслоение комбинированной трехслойной структуры на пять слоев по 8 частиц при T = 0.12.
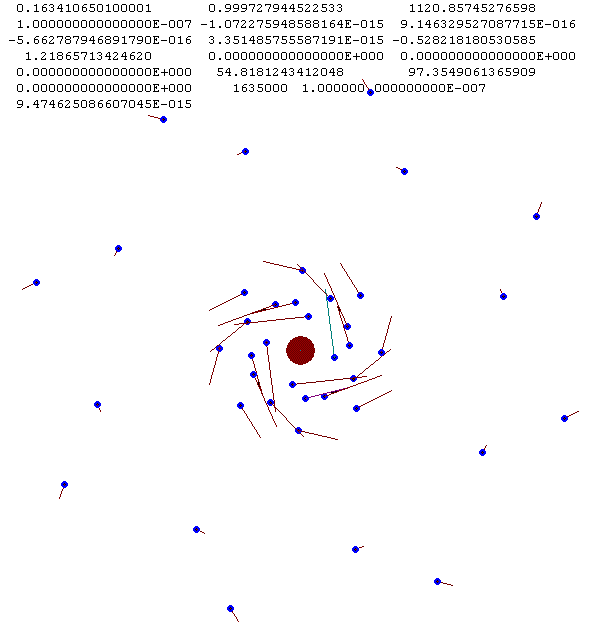
Рис. 33. Дальнейшее расслоение комбинированной трехслойной структуры при T = 0.163.
Далее это движение к центру третьего слоя продолжается, и под его воздействием начинают сжиматься внутренние второй и первый слои. В момент T = 0.1634, как видно из рис. 33, первый слой распадается на два слоя по 4 частицы в каждом. Кроме того, на этом рисунке видно, что увеличивается расстояние между 4-ым и 5-ым слоями. Четвертый слой движется к центру, а пятый увеличивается в размере.
К моменту T = 0.170 два внутренних слоя по 4 частицы в каждом приближаются к центру, а затем меньший из них к моменту T = 0.1841 распадается на два слоя по 2 частицы. К этому времени осевая симметрия заметно нарушается. Начинаются сближения частиц и структура распадается.
Таким образом, рассматриваемая структура существовала без изменений в течение одного оборота внутреннего слоя. Затем она изменялась без разрушения ее целостности. Этот процесс можно также рассматривать как развитие структуры. Оно продолжалось в течение 7 оборотов внутреннего слоя. В начале, расслоились слои, у которых было отличие в скоростях частиц, затем начали расслаиваться слои, у которых появились отличия в результате развития первоначальных возмущений.
Рассмотренная на рис. 31 комбинированная структура демонстрирует возможности программы RtStClb2 по созданию структур, конфигурация которой отличается от первоначально рассмотренной конфигурации с одинаковым числом частиц в слоях. Возможно, эта программа или ее модификация позволит создавать структуры и с другими конфигурациями.
Созданные программой RtStClb2 структуры имеют первоначальные периоды вращения слоев, а, следовательно, и первоначальные скорости, в момент начального взаимного расположения частиц. И как уже отмечалось, смещения частицы на половину угла 0 приводит к отличающимся периодам. Поэтому изменение взаимного расположения частиц, по сравнению с первоначальным, является одной из причин, которые приводят к изменению структуры в процессе ее движения. Этот недостаток можно избежать коррекцией первоначальных периодов. Их нужно задать такими, чтобы средний период обращения частиц в каждом слое не изменялся. Для определения новых периодов необходимо последовательно просчитывать с помощью системы Galactica динамику структуры и определять реальные скорости движения частиц в ней. По средним скоростям за одно обращение частицы будет уточняться величина периода вращения слоя.
Возможно, таким способом удастся создать структуру, в которой происходит стабильное вращение слоев. В работах [10]-[11] отмечено, что в многослойных структурах устойчивость частиц на слое может повышаться по сравнению с однослойной структурой. В этих же работах показано, что увеличение периодов вращения слоя также повышает их устойчивость. По-видимому, дальнейшие исследования покажут реальную возможность создать устойчивую плоскую модель атома или наметить пути преобразования ее в устойчивую пространственную модель.
15. Обсуждение результатов
15.1. Множественные решения в неустойчивой структуре
Как уже отмечалось, рассмотренная четырехслойная структура (рис. 4), является неустойчивой. Все частицы на каждом слое уравновешены одинаково. Поэтому любая из них может выйти из состояния равновесия и по истечению определенного времени система разрушается. При численном решении задачи, в зависимости от варианта вычислительного процесса, происходит начальное смещение разных частиц. В нашем случае вариант вычислительного процесса определялся шагом интегрирования ΔT. Он может также определяться видом компилятора программы при создании исполнительного ее модуля или видом процессора. Во всех этих случаях существуют отличия величин в последних разрядах представляющих их чисел. Эти отличия и создают варианты разрушения системы.
Рис. 34. Находящийся в неустойчивом положении шар может скатываться в любом направлении, например, 1 или 2.
Неустойчивое положение рассмотренной структуры аналогично положению в следующем примере. Представим себе конус (рис. 34), ось которого расположен вертикально. Пусть конус плавно сопрягается с плоскостью, на которой он стоит. Поместим на вершину конуса шар и рассмотрим его движения под влиянием силы тяжести, направленной вниз. Шар находится в неустойчивом положении, и он обязательно скатится вниз. При решении этой задачи мы также будем получать разные варианты направления движения шара, например, 1 или 2, в зависимости от варианта вычислительного процесса. Но во всех вариантах время движения и скорость движения шара будут одинаковы.
В рассмотренном случае структуры, во всех трех вариантах, мы также получили одинаковые динамические показатели до момента ее разрушения. А после разрушения структуры ее динамика определяется начальными возмущениями.
15.2. Механизмы выброса частиц из структуры
После нарушения целостности структуры поведение ее частиц определяется взаимными сближениями. При сближениях частиц силы их взаимодействия становятся определяющими. Динамика каждой частицы зависит от истории ее сближения с другими частицами. Поэтому в многочастичной структуре возможно бесконечное количество поведений частицы. Мы здесь рассмотрели три варианта, при которых частица выбрасывается из структуры. Если структура состоит из двух частиц, т.е. одна движется относительно другой по эллиптической орбите, то ни одна частица не может покинуть эту структуру. В многочастичной структуре выброс частиц возможен. В результате взаимодействий между частицами одни из них могут ускоряться, а другие замедляться. Поэтому в результате наложения нескольких ускорений, частица может приобрести скорость, достаточную чтобы быть выброшенной из структуры.
В первых двух рассмотренных случаях выбрасываемая из структуры частица находится в апоцентрии. Между ней и притягивающим центром проходит частица, которая тормозит ее и в значительной степени уменьшает ее трансверсальную скорость. Поэтому первая частица почти радиально движется к центру и при прохождении на малом расстоянии от него приобретает большую скорость. Эта скорость может быть достаточной, чтобы частица была выброшена из структуры.
В этих двух вариантах: торможение частицы 11 на рис. 9 и частицы 2 на рис. 14 происходит после достижения апоцентрия. В третьем варианте торможение частицы 7 частицей 1 (рис. 22) происходит несколько по-другому. Последняя частица проходит за апоцентрием A1 частицы 7, но также тормозит ее еще при подходе к апоцентрию. Затем частица 7 (рис. 22) совершает одно обращение по уменьшенной орбите и в апоцентрии A2 снова испытывает торможение частицей 1. В последнем приближении к перицентрию она приобретает скорость 33600, с которой и выбрасывается из структуры. Вследствие такого двухступенчатого торможения эта скорость выброса меньше скорости выброса в первых двух случаях. Следует напомнить, что скорость выброса была уточнена только в первом варианте, а в остальных вариантах она не уточнялась.
15.3. Необычные явления при взаимодействиях
Как уже отмечалось, после разрушения упорядоченной структуры возможны множественные поведения частиц. В третьем варианте было зафиксировано уникальное явление: смена направления обращения частицы 4 (рис. 26a). Механизм его показан на рис. 35. В момент T = 0.3343 положения частиц 4, 13 и 18 показано мелким шрифтом цифрой 1, а последующие положения этих частиц - цифрами от 2 до 6. Частица 4 в положении 2 сталкивается с частицей 13 и почти на 90° изменяет свое направление движения. Затем происходит ее столкновение с частицей 18 в положении 4 и снова направление ее движения изменяется в ту же сторону, но на меньший угол, порядка 60°. В результате этих двух столкновений частица 4 начала обращаться по часовой стрелке. Из рис. 35 видно, что частицы 13 и 18 при этом также значительно изменяют свои направления движения: частица 13 - на ~ 330°, а частица 18 - на ~ 90°. Кроме того частица 18 до столкновения уже обращалась по часовой стрелке, а частица 13 после столкновения начинает обращение по часовой стрелке. В тоже время частица 18 после столкновения начинает обращаться против часовой стрелки. Таким образом, все три частицы в результате двух столкновений поменяли направления своих обращений.
Рис. 35. Последовательные положения частиц 4, 13 и 18 на плоскости xy в третьем варианте на интервале времени T от 0.3343 до 0.3375. Шесть положений тел от 1 до 6, мелким шрифтом, и соответствующие моменты времени указаны на рисунке. | 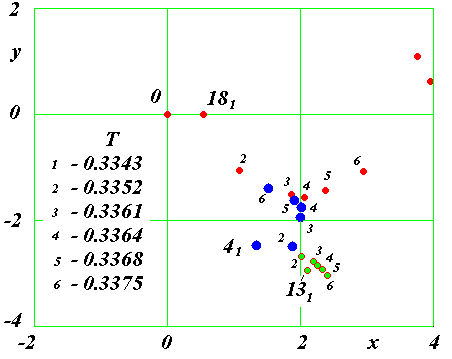 |
Последнее необычное явление - это прямое столкновение частицы 4 с центральной (рис. 26). Вероятность прямого столкновения частиц, учитывая их малые размеры, является очень малой. Как видим, в данном случае (рис. 27) оно происходит после 7 обращений вокруг центральной частицы. Небольшее воздействие частицы 10 на последнем обращении (рис. 25b) уменьшает прицельное расстояние частицы 4 по отношению к центральной частице 0, и она сталкивается с последней.
Взаимодействия многих частиц, как показано выше, приводят к разнообразным явлениям, только малая часть из которых была здесь рассмотрена. Многие из этих явлений, не столкнувшись с ними, представить заранее невозможно. Аналогичные случаи взаимодействий могут наблюдаться при вхождении частицы в существующую структуру. Поэтому при исследовании таких структур, как атомы и молекулы, при проникновении в них посторонних частиц, будут встречаться разнообразные явления. Если не знать их истинной причины, а интерпретировать на основании двухчастичных взаимодействий, проникающей частицы и ядра, то результаты такой интерпретации будут давать неверные представления об устройстве микромира.
15.4. Дальнейшие поиски устойчивых структур
Выполненные исследования показали, что рассмотренные плоские структуры длительно не могут существовать. Полученные в результате точного решения уравнений взаимодействия частиц [10]-[11] однослойные осесимметричные кулоновские структуры, являются неустойчивыми и через несколько обращений распадаются. В этих решениях орбиты частиц могут быть не только окружности, но и эллипсы, параболы и гиперболы.
Многослойные осесимметричные вращающиеся как единое целое структуры не могут быть получены в результате точного решения уравнений взаимодействия. То есть, решений для таких конфигураций не существует. Можно создать структуры с определенным числом слоев и частиц на каждом слое, если слои вращаются с разными угловыми скоростями. Возможны разные алгоритмы задания периодов вращения слоев. В работе периоды заданы из условия, что в начальный момент структура является осесимметричной и обращение частиц происходит по окружностям. Однако в процессе вращения слоев с разными периодами осевая симметрия нарушается, силы воздействия на частицы в слоях изменяются, и они движутся по эллиптическим орбитам. Положение частиц на слоях является неустойчивым. Частицы уходят с этих положений. Затем происходят процессы сближения частиц между собой. При сближениях силы взаимодействия многократно увеличиваются, что приводит к быстрому разрушению всей системы.
На основании полученных результатов можно развить другие алгоритмы задания периодов вращения слоев. Например, можно подобрать такие периоды, чтобы радиусы слоев не изменялись. Однако неустойчивые положения частиц в каждом слое приводит к его разрушению. В многослойных структурах устойчивость в слоях повышается. Повышается устойчивость структур с увеличением периодов вращения слоев. Необходимо искать конфигурации структур с увеличенным временем жизни.
При пространственной организации слоя на орбите может находиться одна частица, а орбиты остальных частиц развернуты в пространстве относительно друг друга. Чтобы не происходило сближения частиц, фазы их должны быть равномерно распределены по периоду. Алгоритм создания такой структуры может быть основан на алгоритмах, использованных в настоящей работе.
Если удастся создать пространственную устойчивую структуру, то фазы и периоды движений всех частиц должны быть согласованы между собой. В противном случае произойдет сближение частиц и структура разрушится. В случае изменения размеров структуры периоды движений должны изменяться ступенчато, чтобы сохранить согласованность движений. Возможно, в этом и заключается суть квантованных состояний.
15.5. Границы применимости результатов
Полученные скорости выброса частиц превышают скорость света, которая в использованных безразмерных единицах = 2.10939·104. Закон Кулона определяет силу взаимодействия частиц в неподвижном состоянии. Как только появляется движение одной частицы относительно другой, сила их взаимодействия изменяется. Исторически сложилось так, что непосредственное изменение силы при движении не изучалось, а исследовалось магнитное воздействие заряженных частиц, появляющееся при наличии их движения. В теории относительности дополнительное магнитное воздействие учитывают зависимостью массы, времени и длины от скорости. Этот подход, во-первых, неверен с позиций механики, а, во-вторых, неточен с позиций электродинамики [17], [18]. Правильный учет магнитного воздействия заряженной частицы qi на частицу с зарядом qj осуществляется в следующем выражении для силы:
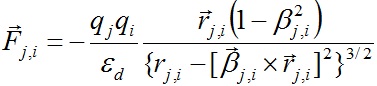 , , | (40) |
где 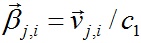 ;
;
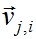 - вектор скорости частицы qi относительно частицы qj;
- вектор скорости частицы qi относительно частицы qj;
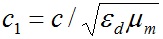 ;
;
μ m - магнитная проницаемость среды, в которой находятся частицы.
В отличие от закона Кулона (3) сила (40) зависит не только от расстояния rj,I, но и от скорости vj,i частицы i относительно частицы j.
При взаимодействии, определяемом выражением (40), скорость частицы не может превысить скорость света. Например, при радиальном кулоновском взаимодействии двух частиц радиальная скорость (формула (5.27) [17]) определяется выражением
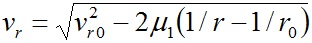 , , | (41) |
где 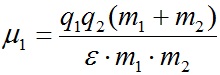 - параметр взаимодействия двух частиц;
- параметр взаимодействия двух частиц;
r0 - начальное расстояние между частицами, при котором радиальная скорость частицы была vr0.
При взаимодействии (40) радиальная скорость в этом случае движения будет (формула (4.80) [17]):
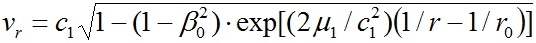 . . | (42) |
Выражение (41) в рассмотренных случаях сближения частиц даст сверхсветовые скорости, а выражение (42) - досветовые.
Исследования [17], [19]-[21] показали, что до скоростей движения частиц v < 0.1c расчеты взаимодействия по закону Кулона мало отличаются от расчетов по точному выражению для силы (40). В безразмерных единицах значение скорости, при котором можно использовать закон Кулона, является v = 0.1c = 2110. Наибольшая скорость частиц в начальный момент движения в четырехслойной структуре (рис. 4) равна 720, а перед ее разрушением - не превышает 1000. Поэтому полученные результаты по динамике структуры и начальным этапам ее разрушения на основе кулоновского закона существенно не изменятся при точном законе взаимодействия (40). А величины скоростей, которые получаются при близких сближениях частиц, требуют коррекции. В дальнейшем мы планируем дополнить систему Galactica модулем, который позволял бы точно рассчитывать взаимодействия заряженных частиц во всем диапазоне скоростей их движения.
Следует отметить, что в случае взаимодействия многих частиц по закону (40) отдельные частицы также могут достигать сверхсветовой скорости. Например, если одна частица, движущаяся со скоростью близкой к скорости света, догоняет вторую частицу и ускоряет ее, то вторая частица может превысить скорость света [22].
15.6. Основные выводы
Гравитационные взаимодействия полностью объясняют явления, происходящие в макромире [23]-[24]. В этом человек постоянно убеждается на протяжении последних нескольких сот лет. Предстоит такая же работа по объяснению микромира кулоновскими взаимодействиями. Чтобы проинтегрировать дифференциальные уравнения движения при взаимодействии частиц, необходимо задать их координаты и скорости. Координаты частиц могут быть заданы, если известна геометрия системы. Скорости частиц должны быть таковыми, чтобы эта геометрия не разрушалась при дальнейшем взаимодействии. В случае взаимодействия двух частиц координаты и их скорости могут быть заданы на основании решения задачи 2-х тел. В случае N-тел проблему задания начальных условий часто решить невозможно. Поэтому мы рассматриваем структуры из N частиц, для которых можно получить точное решение задачи их кулоновского взаимодействия. В работе эти решения получены, что позволило получить ряд структур. С помощью системы Galactica исследована их динамика и устойчивость. Полученные структуры являются неустойчивыми. Намечены пути по поиску устойчивых структур.
Благодарности
Вычисления для большого количества частиц выполнялись на суперкомпьютерах Сибирского суперкомпьютерного центра СО РАН, г. Новосибирск.
Литература
Приложение. Описание программы и ее работы, содержание файла исходных данных и текст программы для решения задачи о плоских многослойных кулоновских структурах
1. Описание программы
Программа RtStClb2.for предназначена для расчета периодов Prdj вращения слоев плоской многослойной структуры, заряженные частицы в которой взаимодействуют по закону Кулона. Кроме того, она позволяет подобрать необходимые параметры, определяющие конфигурацию структуры. И дополнительно, программа RtStClb2.for подготавливает файл исходных и начальных данных для программы Galactica, которая имеется в свободном доступе [9], [12] и [13]. Система Galactica позволяет рассчитать динамику многослойной вращающейся структуры и исследовать ее эволюцию.
Программа RtStClb2.for написана на языке FORTRAN. Параметры структуры задаются в файле ее исходных данных RtStClb2.dat. Эти файлы приведены ниже. В файле данных RtStClb2.dat задаются параметры многослойной структуры (см. внизу). Структура создается с учетом физических свойств нейтрального атома в виде трех групп данных. В первой группе задается количество колец N2, количество частиц N3 на каждом кольце и массового числа ядра nA. Величина nA определяет количество протонов и нейтронов в ядре.
Во второй группе данных задаются константы: массы протона (cmp), электрона (cme) и нейтрона (cmne) в кг; модуль заряда электрона (ee) и диэлектрическая постоянная среды (ed), в которой находятся частицы. Два последних параметра задаются в системе СГСЭ. Единица времени (UnT) задается в секундах.
В третьей группе данных задается геометрическая конфигурация структуры. Имеется два способа задания геометрии структуры. В первом способе предлагаются алгоритмы ее задания, а во втором способе пользователь может задать любую геометрию структуры. Радиусы структуры rj могут быть заданы по алгоритму (37) с помощью параметра okr. А углы первых тел на кольцах на слоях φj,1 могут быть заданы в двух вариантах: при Ivr = 1 φj,1 = 0; при Ivr = 2 углы первых тел на слоях чередуются: φj,1 = 0 и φj,1 = Δφ0.
Любая геометрия структуры задается в файлах. Радиусы rj задаются в файле, имя которого определяется в переменной FIMA2. В файле содержится два столбца: j и rj. А углы φj,1 в таком же виде задаются в файле RtStCfi0.dat. Подключение этих файлов осуществляется при задании значения 1 для ключей Kl1 и Kl3.
Шестой параметр Prdi в третьей группе задает начальный период вращения первого кольца. После работы программы период вращения первого кольца будет рассчитан точно. По величине Prdi согласно (34) определяется геометрический параметр R0, к которому нормированы безразмерные радиусы слоев в программе RtStClb2.for. Поэтому начальный период вращения первого слоя Prdi определяет размер структуры. Чем он больше, тем больше диаметр структуры.
Последние четыре параметра в файле данных RtStClb2.dat: eps0, dt, FIMA5, Idta необходимы для создания файла исходных данных и начальных условий для решения дифференциальных уравнений движения тел многослойной структуры с помощью программы Galactica. Углом eps0 в радианах задается наклон плоскости структуры к некоторой плоскости, которая названа плоскостью экватора. С помощью этого угла двумерная структура пересчитывается в трехмерную. Поэтому в программе Galactica динамика многослойной структуры решается по трем координатам. Параметром dt в единицах UnT задается номинальный шаг интегрирования в программе Galactica. Параметрами FIMA5 и Idta задается имя файла начальных условий и время его создания. Структура этого файла приведена в работе [9], а также - в Описании системы Galactica [13].
2. Работа программы
После запуска исполняемого модуля программы RtStClb2.exe и завершения его работы создается 3 файла: RtStCfi1.dat, ErRtClSt.dat и, как пример, B205c08p.dat. В файле RtStfi1.dat записаны номера колец j и углы первых тел φj,1. Этот файл может быть взят за основу файла RtStfi0.dat, в котором может быть задана любая конфигурация углов первых тел. Файл ErRtClSt.dat является файлом ошибок и сообщений. Эти сообщения выдаются одновременно на дисплей и в этот файл. Сообщения об ошибках работы процессора выдаются только на дисплей. Самой распространенным сообщением является сообщение об отрицательном знаменателе в выражении (33): (nZ - As) < 0 для слоя j. Файл начальных условий для программы Galactica в этом случае не создается.
При отсутствии ошибок в файл ErRtClSt.dat записываются номера колец j и относительные их радиусы 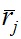 и периоды
и периоды 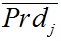 , а, также согласно (21) и (23), коэффициенты aj,i уравнений (33). В этом случае также создается файл начальных условий для программы Galactica, имя которого, например B205c08p.dat, задано в файле RtStClb2.dat.
, а, также согласно (21) и (23), коэффициенты aj,i уравнений (33). В этом случае также создается файл начальных условий для программы Galactica, имя которого, например B205c08p.dat, задано в файле RtStClb2.dat.
В файле начальных условий B205c08p.dat приводятся исходные данные и начальные условия для исследования динамики образованной структуры с помощью системы Galactica. Детальное описание этого файла и системы Galactica даны в отмеченных ранее источниках [9], [12]-[13]. В названии этого файла отмечены свойства его структуры: второй вариант начального угла первого тела кольца, 5 колец и 8 частиц на каждом кольце.
Как уже отмечалось, бывают случаи параметров структуры, когда знаменатель (33) для кольца j становится отрицательным. Это означает, что силы отталкивания между электронами преобладают над силой притяжения к ядру. В этом случае необходимо изменять, как правило, увеличивать радиус кольца rj.
3. Содержание файла исходных данных RtStClb2.dat
| No | Описание параметра | Пара-метр | Величина,начиная с 60 позиции |
| 1 | The number of rings 16.10.2014 | N2 | 5 |
| 2 | The number of bodies in the ring | N3 | 8 |
| 3 | The mass number of the atomic nucleus | nA | 80 |
| 4 | Constants | ||
| 5 | Mass of proton | cmp | 1.67252D-27 |
| 6 | Mass of electron | cme | 9.10910D-31 |
| 7 | Mass of neutron | cmne | 1.67482D-27 |
| 8 | Charge of electron | ee | 4.80298D-10 |
| 9 | Dielectric permittivity of the medium | ed | 1.00000D+0 |
| 10 | Unit of time | UnT | 1.00000D-15 |
| 11 | Other parameters of atom | ||
| 12 | Coefficient of initial radii of rings | okr | 1.00000D-0 |
| 13 | Key of input of radii from file FIMA2 | Kl1 | 1 |
| 14 | The file name with initial radii | FIMA2 | RtNcJR01.dat |
| 15 | Variant of angles of first bodies in rings | Ivr | 2 |
| 16 | Angles of 1-st bodies from file RtStCfi0.dat | Kl3 | 0 |
| 17 | Initial period of revolution in units of time | Prdi | 3.29471D-2 |
| 18 | Angle of inclination of the rings to equator | eps0 | 0.40900D+0 |
| 19 | Step time integration | dt | 1.00000D-7 |
| 20 | The initial data file name | FIMA5 | B205c08p.dat |
| 21 | Creation date of the initial conditions file | Idta | 20150127 |
4. Текст программы RtStClb2.for
C*********************************************************************
C* ***** RtStClb2.for *****
C Многослойные кулоновские структуры с дифференциальным вращением
C Joseph J. Smulsky
C Последнее изменение 18 ч. 00 м. 02.02.2015 г.
C*********************************************************************
C---------------------------------------------------
C Нужно задать значения параметров!
PARAMETER (l2=1000,l4=6000) !
C ---------------------------------------------------
IMPLICIT DOUBLE PRECISION (A-H,O-Z)
DIMENSION A1(l2,l2+1),fi(l2,l2),cm(l2),
*R(l2),Ro(l2),qo(l2),Prd(l2),wo(l2),
*omo(l2*l2+1),Xo(l2*l2+1,3),Uo(l2*l2+1,3),X1(l2*l2+1,3),
*U1(l2*l2+1,3),Pns(3),Xc(3),AM1(3),Pn(3),X(l2*l2+1,3),
*U(l2*l2+1,3),Sp(l2*l2+1,3),Et(l2*l2+1),Ra(l2*l2+1),dUp(l2*l2+1,3)
INTEGER*4 N,Nstr,N2,N3,Idta,q
CHARACTER*12 FIMA1,FIMA2,FIMA3,FIMA4,FIMA5,FIMA6,FIMA7
FIMA1 ='RtStClb2.dat'
FIMA3 ='ErRtClSt.dat'
FIMA4 ='RtQNcREr.dat' ! Номер кольца, радиус кольца, ошибка
FIMA6 ='RtStCfi0.dat'
FIMA7 ='RtStCfi1.dat'
C--- Считывание файла RtStClb2.dat.
OPEN(UNIT=1,FILE=FIMA1,STATUS='OLD')
READ(1,39,ERR=40)N2
READ(1,39,ERR=40)N3
READ(1,39,ERR=40)nA
READ(1,55,ERR=40)Tmp
READ(1,54,ERR=40)cmp
READ(1,54,ERR=40)cme
READ(1,54,ERR=40)cmne
READ(1,54,ERR=40)ee
READ(1,54,ERR=40)ed
READ(1,54,ERR=40)UnT
READ(1,55,ERR=40)Tmp
READ(1,54,ERR=40)okr
READ(1,39,ERR=40)Kl1
READ(1,'(59X,A12)',ERR=40)FIMA2
READ(1,38,ERR=40)Ivr
READ(1,38,ERR=40)Kl3
READ(1,54,ERR=40)Prdi
READ(1,54,ERR=40)eps0
READ(1,54,ERR=40)dt
READ(1,'(59X,A12)',ERR=40)FIMA5
READ(1,39,ERR=40)Idta
CLOSE(1)
38 FORMAT(59X,I5)
39 FORMAT(59X,I12)
53 FORMAT(59X,F11.4)
54 FORMAT(59X,D11.5)
55 FORMAT(2X,D10.4)
GO TO 1
40 WRITE(*,*)'*01Rt Error reading file RtStClb2.dat *** ',
*N2,N3,nA,cmp,cme,cmne,ee,ed,UnT,okr,Kl1,Ivr,Kl3,Prdi,
*eps0,FIMA5,Idta
OPEN(UNIT=3,FILE=FIMA3)
WRITE(3,*)'*01Rt Error reading file RtStClb2.dat *** ',
*N2,N3,nA,cmp,cme,cmne,ee,ed,UnT,okr,Kl1,Ivr,Kl3,Prdi,
*eps0,FIMA5,Idta
CLOSE(3)
GO TO 150
1 pi = 3.1415926535897932385D+00
p2 = 2.0D+00*pi
DZI = 0.0D+00
PND = 1.5D+00
PND2 = 1.0D+00/3.0D+00
dfi0 = p2/N3
C--- Constants from Handbook by Yavorsky & Detlaf: pp.749, 910, 912, 913.
C cmp = 1.67252D-27
C cme = 9.10910D-31
C cmne = 1.67482D-27
C ee = 4.80298D-10
C Prd0 = 3.294713055979042D-17
C Prd0 = 1.0D-15
Prdsc = Prdi*UnT
nZ = N2*N3
qo0 = nZ
qo1 = -1
N23 = N2*N3
Nne = nA - nZ
cm0 = nZ*cmp + Nne*cmne
Rn0 = 1.5D-15
Re = 1.5D-15
Rn = Rn0*(nA**PND2)
TMP = 1.0D-9*ee*ee*Prdsc*Prdsc/(4*pi*pi*ed*cme)
R0 = TMP**PND2
okt = 1/UnT
C WRITE(*,*)'*01*** ',R0,Prdi,Prdsc
ssm = cm0
DO J = 1,N2
cm(J) = cme
ssm = ssm + cm(J)*N3 !!-1str
END DO ! J
TMP = 1.0D-9*ee*ee/(ed*ssm*okt*okt)
Am = TMP**PND2
okv = 1/(okt*Am)
N = N2*N3 + 1
Nstr = l4/2
k1 = 1
fn3 = DZI
DO l = 2,N3
fn3 = fn3 + 0.25D+0/DSIN((l-1)*pi/N3)
END DO ! l
C--- Углы первых тел на кольцах
IF(Ivr.EQ.1) THEN
DO I = 1,N2
fi(I,1) = DZI
END DO ! I
ELSE
I2 = 0
DO I = 1,N2
I2 = I2 +1
fi(I2,1) = DZI
I2 = I2 +1
fi(I2,1) = 0.5D+0*dfi0
IF(I2.EQ.N2) GO TO 3
END DO ! I
3 END IF ! Ivr
C--- Углы первых тел на кольцах из файла RtStCfi0.dat.
IF(Kl3.EQ.1) THEN
OPEN(UNIT=6,FILE=FIMA6)
DO I = 1,N2
READ(6,*)I1,fi(I,1)
END DO ! I
CLOSE(6)
ELSE
OPEN(UNIT=7,FILE=FIMA7)
DO I = 1,N2
WRITE(7,*)I,fi(I,1)
END DO ! I
CLOSE(7)
END IF !
C--- Углы всех тел на кольцах
DO J = 1,N2
DO l = 2,N3
fi(J,l) = fi(J,l-1) + dfi0
END DO ! l
END DO ! J
C--- Радиусы колец, отнесенные к R0.
IF(Kl1.EQ.1) GO TO 27
R(1) = (nZ - fn3)**PND2
OPEN(UNIT=3,FILE=FIMA3)
WRITE(3,*) 'Devided on R0 radii of the circles'
WRITE(3,*) ' 1 ',R(1)
DO I = 2,N2
R(I) = okr*I*R(1)
WRITE(3,*) I,R(I)
END DO ! I
CLOSE(3)
GO TO 11
27 OPEN(UNIT=2,FILE=FIMA2)
DO J = 1,N2
READ(2,*)J1,R(J)
END DO ! J
CLOSE(2)
C--- Cила Qs воздействия на тело кольца j всех тел всех колец
C--- В RtStClb2_0.for Qs - на кольцо j не учитывалось действие нар. колец
11 DO J = 1,N2
As = DZI
C DO I = 1,J ! Было в RtStClb2_0.for
DO I = 1,N2
Qs = DZI
RIJ = R(I)/R(J)
DO l = 1,N3
dfi = fi(I,l) - fi(J,1)
C--- Предотвращение деления на нуль в случаях
C--- сил воздействия тела на себя.
IF(l.EQ.1.AND.I.EQ.J) dfi = pi
C--- Расчет сил воздействия на тело данного кольца тела другого кольца
TMP = RIJ*DCOS(dfi)
Q1 = (1-TMP)/(1+RIJ*RIJ-2*TMP)**PND
C--- Обнуление сил воздействия тела кольца на себя.
IF(l.EQ.1.AND.I.EQ.J) Q1 = DZI
Qs = Qs + Q1
END DO ! l
A1(J,I) = Qs
As = As + A1(J,I)
END DO ! I
R3 = R(J)*R(J)*R(J)
TMP = nZ - As
IF(TMP.GT.DZI) GO TO 12
OPEN(UNIT=3,FILE=FIMA3)
WRITE(*,*)'*02Rt Error: (nZ - As) < 0 *** ',TMP,' J = ',J, ! 02.02.2015
*' R(J) = ',R(J)
OPEN(UNIT=3,FILE=FIMA3)
WRITE(3,*)'*02Rt Error: (nZ - As) < 0 *** ',TMP,' J = ',J, ! 02.02.2015
*' R(J) = ',R(J)
CLOSE(3)
GO TO 150
12 Prd(J) = DSQRT(R3/TMP)
wo(J) = p2/(Prd(J)*Prdsc*okt)
END DO ! J
OPEN(UNIT=3,FILE=FIMA3)
WRITE(3,*)'Relative radii (R(I)/R0) of the circles and periods'
DO I = 1,N2
WRITE(3,*) I,R(I),Prd(I)
END DO ! I
WRITE(3,*) 'Coefficients A1(J,I) of the equations'
DO J = 1,N2
WRITE(3,15) J,(A1(J,I),I=1,N2)
END DO ! J
CLOSE(3)
15 FORMAT(I5,20E13.4)
C--- Массы тел в программе Galactica и параметры в плоскости орбиты
omo(1) = cm0/ssm
qo(1) = qo0
Ra(1) = Rn/Am
k = 1
DO J = 1,N2
Ro(J) = R(J)*R0/Am
DO l = 1,N3
k = k+1
omo(k) = cm(J)/ssm
qo(k) = qo1
Ra(k) = Re/Am
Xo(k,1) = Ro(J)*DCOS(fi(J,l))
Xo(k,2) = Ro(J)*DSIN(fi(J,l))
Xo(k,3) = DZI
Uo(k,1) = -Ro(J)*wo(J)*DSIN(fi(J,l))
Uo(k,2) = Ro(J)*wo(J)*DCOS(fi(J,l))
Uo(k,3) = DZI
END DO ! l
END DO ! J
C--- Координаты и скорости периферийных тел в экваториальной плокости
DO k = 2,N
X1(k,1) = Xo(k,1)
X1(k,2) = Xo(k,2)*DCOS(eps0) - Xo(k,3)*DSIN(eps0)
X1(k,3) = Xo(k,2)*DSIN(eps0) + Xo(k,3)*DCOS(eps0)
U1(k,1) = Uo(k,1)
U1(k,2) = Uo(k,2)*DCOS(eps0) - Uo(k,3)*DSIN(eps0)
U1(k,3) = Uo(k,2)*DSIN(eps0) + Uo(k,3)*DCOS(eps0)
END DO ! k
C--- Координаты и скорости центрального тела в экваториальной плокости
DO q = 1,3
X1(1,q) = DZI
U1(1,q) = DZI
END DO ! q
C--- Параметры центра масс.
30 DO q = 1,3
Pns(q) = DZI
Xc(q) = DZI
AM1(q) = DZI
END DO ! q
DO k = k1,N
IF(omo(k).EQ.DZI) GO TO 32
DO q = 1,3
Xc(q) = Xc(q) + omo(k) * X1(k,q)
Pn(q) = omo(k) * U1(k,q)
Pns(q) = Pns(q) + Pn(q)
END DO ! q
32 END DO ! k
C--- Приведение к центру масс.
DO k = k1,N
IF(omo(k).EQ.DZI) GO TO 16
DO q = 1,3
X(k,q) = X1(k,q) - Xc(q)
U(k,q) = U1(k,q) - Pns(q)
END DO ! q
AM1(1) = AM1(1)-omo(k)*U(k,2)*X(k,3)+omo(k)*U(k,3)*X(k,2)
AM1(2) = AM1(2)+omo(k)*U(k,1)*X(k,3)-omo(k)*U(k,3)*X(k,1)
AM1(3) = AM1(3)+omo(k)*U(k,2)*X(k,1)-omo(k)*U(k,1)*X(k,2)
16 END DO ! k
DO q = 1,3
Pns(q) = DZI
END DO ! q
omm = DZI
DO k = k1,N
DO q = 1,3
Pn(q) = omo(k) * U(k,q)
Pns(q) = Pns(q) + Pn(q)
dUp(k,q) = DZI
Sp(k,q) = DZI
END DO ! q
Et(k) = DZI
IF(omo(k).LT.omm) GO TO 13
omm = omo(k)
13 END DO ! k
A = 1.0D+0
B = 0.5D+0
C = 0.25D+0
TMP = (N+1)**PND2
Mu = NINT(TMP)
T = DZI
Um = DZI
Spsx = DZI
Spsy = DZI
Spsz = DZI
E = DZI
Em = DZI
Ett = DZI
dtp = DZI
C--- Создание файла начальных условий FIMA5 для программы Galactica.
OPEN(UNIT=5,FILE=FIMA5)
WRITE(5,*)T,omm,Um,dtp,Pns(1),Pns(2),Pns(3),AM1(1),AM1(2),
*AM1(3),Spsx,Spsy,Spsz,E,Em,Ett,dt,1,1,N,A,B,C,Mu,ed
DO k = k1,N
WRITE(5,*) omo(k),(X(k,q),q=1,3),(U(k,q),q=1,3),
*(dUp(k,q),q=1,3),(Sp(k,q),q=1,3),Ra(k),Et(k),qo(k)
END DO ! k
C--- Information line at end of file
WRITE(5,*)Idta,N,ssm,Am,okv,0,0,0,0,0,0,0,0,0,0,0
CLOSE(5)
150 CONTINUE
END
------------------------------------------------------------------------------------------------------------------
Печатается в соответствии с решением Ученого Совета Института криосферы Земли
Сибирского отделения Российской академии наук от 20 февраля 2015 г., протокол № 2.